Calculate Angular Velocity After Ball-Rod Collision

[Nirmal]

Homework Statement

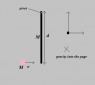
To understand the question first see the attachment (picture). The ball hits the rod and then it sticks to the end opposite the pivot. So now what is the angular velocity (ω) just after collision.

Homework Equations

1/2m_1v_1^2 + 1/2 I_1ω_1^2 = 1/2mv^2 + 1/2 Iω^2 (conservation of kinetic energy)
I_1ω_1 = I_2ω_2 (conservation of momentum)
I at centre of mass of rod = ML^2/12 where L is the length of rod
I at edge of rod = ML^2/3 where L is the length of rod

The Attempt at a Solution

By conservation of kinetic energy
1/2 M V^2 + 0 = 1/6 M d^2 ω^2 + 0
SO ω = v*sqrt(3)/(d)

 

[Simon Bridge]

You have to ask a question :)

I have a couple for you though:
What leads you to believe that kinetic energy is conserved in this collision?
Did you try checking your result by conservation of angular momentum?

 

[Nathanael]

You can't use conservation of kinetic energy, because kinetic energy is not conserved in inelastic collisions. Some energy will be lost in some way (I would assume most of the lost energy goes towards deforming the ball).


Use conservation of angular momentum. (What is the angular momentum of a ball moving in a straight line?)



edit:
Simon beat me by a hair :tongue:

 

[Nirmal]

So how would i do that..
angular momentum of a ball moving in a straight line is zero right. SO is the answer of w = o . Is that right. Or if i am wrong please help me.

 

[Nathanael]

No it's not zero. Objects moving linearly also have angular momentum (with respect to a point).

I probably won't explain it well, so here's a short explanation

 

[Nirmal]

Ok is the answer w = 12v/(7d^2) or is it 3v/d^2

 

[Nathanael]

Ok is the answer w = 12v/(7d^2) or is it 3v/d^2

Can you explain a little bit about where your answers come from?


P.S.
Your answers have the wrong units

 

[Nirmal]

MV + 0 = 0 + I w

So here I = Md^2 /3
If a ball is sticked to the end of rod then I becomes Md^2 /3 + Md^2/4 = 7Md^2/12
So solving we get w = 12v/(7d^2)

 

[Nathanael]

MV + 0 = 0 + I w

So here I = Md^2 /3
If a ball is sticked to the end of rod then I becomes Md^2 /3 + Md^2/4 = 7Md^2/12
So solving we get w = 12v/(7d^2)

The angular momentum of the ball before the collision (with respect to the pivot) is not MV (those units are wrong) it is actually MVd (refer to the link in the other post)



Edit: sorry I made a mistake in this post originally. (I was thinking the pivot axis was in the middle)

 

[Nirmal]

The angular momentum of the ball before the collision (with respect to the pivot) is not MV (those units are wrong) it is actually MVd/2 (refer to the link in the other post)

But the rod is pivoting at end of rod not at the centre of mass.

 

[Nathanael]

But the rod is pivoting at end of rod not at the centre of mass.

Yes, you are correct (I just realized my mistake and edited my post right before this).

It would actually be Mvd

 

[Nirmal]

So will the answer be w=12v/7d

 

[Nirmal]

Yes, you are correct (I just realized my mistake and edited my post right before this).

It would actually be Mvd

But 12v/7d is not the correct answer.. I checked it and i got wrong. So what can be the answer.

 

[Nirmal]

You have to ask a question :)

I have a couple for you though:
What leads you to believe that kinetic energy is conserved in this collision?
Did you try checking your result by conservation of angular momentum?

Can you help me ..

 

[Nathanael]

But 12v/7d is not the correct answer..

Why do you say the rotational inertia of the ball is $\frac{md^2}{4}$?

It should be $md^2$

 

[Nirmal]

Why do you say the rotational inertia of the ball is $\frac{md^2}{4}$?

It should be $md^2$

Yes. That was the mistake. Now i realize. Thank you