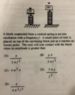Fontseeker
- 30
- 4
Homework Statement
Homework Equations
U = (1/2)kx^2
T = 2 * π * (m/k)^ (1/2)
The Attempt at a Solution
[/B]
T = 2 * π * (m/k)^ (1/2)
T ^ 2 = 4 * π^2 * (m/k)
k = (4 * π^2 * m) / T^2
So I know the initial potential energy is:
U = (1/2)kx^2
U = (1/2)x^2 * ((4 * π^2 * m) / T^2)
However, I don't know how to find where the rock and the spring separate?