rafaamcarvalho
- 3
- 0
Hello to all, first sorry about any mistakes because English is not my native language. I'm trying to solve this problem and I can't seem to find the equation of motion
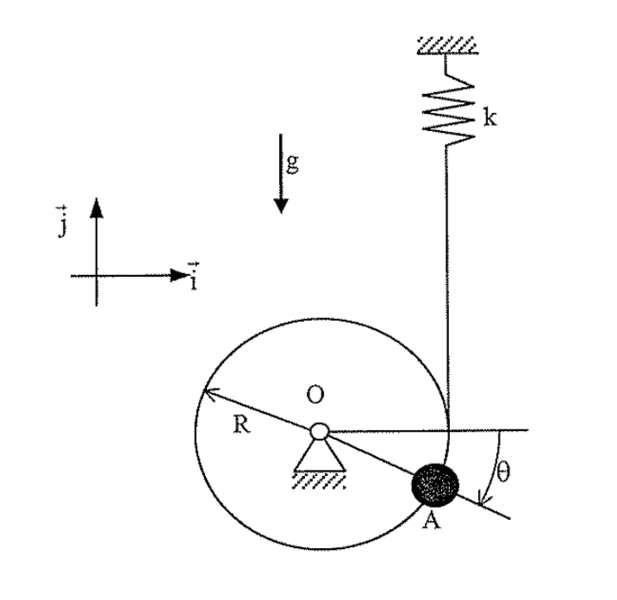
The disc and the point A both have mass m;
θ(0) = 0
2. The attempt at a solution
I tried to use the Newton's second law for rotation but I can't find the values of the point A and K in therms of θ.
I don't know if what I did here was correct, but I tried this:
ΣMo = Jα
Jα = m⋅g⋅r - k⋅x⋅r; x = r⋅sinθ
Homework Statement
The disc and the point A both have mass m;
θ(0) = 0
2. The attempt at a solution
I tried to use the Newton's second law for rotation but I can't find the values of the point A and K in therms of θ.
I don't know if what I did here was correct, but I tried this:
ΣMo = Jα
Jα = m⋅g⋅r - k⋅x⋅r; x = r⋅sinθ