Understanding Parallel Springs & the Equal Extension Assumption"

  • Thread starter Thread starter andyrk
  • Start date Start date
  • Tags Tags
    Parallel Springs
AI Thread Summary
In the discussion on parallel springs, the effective spring constant is derived using the formula keff = k1 + k2, which assumes equal extension in the springs. This assumption is based on the scenario where two adjacent blocks connected by springs are pulled apart, causing both springs to stretch equally. The equal extension is crucial for the derivation, as it simplifies the analysis of the system's behavior under tension. The rationale is that when the blocks are pulled evenly, the forces acting on both springs are balanced, leading to uniform extension. Understanding this concept is essential for accurately analyzing systems involving parallel springs.
andyrk
Messages
658
Reaction score
5
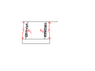
When springs in parallel are replaced by a new spring of a new effective spring constant, for the proof of this, i.e
keff=k1+k2​

Why do we assume the extension in the springs to be equal?
 
Physics news on Phys.org
If you imagine two adjacent blocks being held together by two springs, if you stretch the blocks apart, the springs stretch equally.
 
In the attachment, why is the extension of the springs same?
 

Attachments

  • Springs in Parallel.png
    Springs in Parallel.png
    3.7 KB · Views: 414
For the sake of the derivation, you assume that the little block is pulled evenly so that both springs are extended the same amount.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Finding effective spring constants
Replies
2
Views
4K
Torque in a parallel combination of springs
Replies
8
Views
1K
Irodov- 1.123- Simple conceptual question with two masses connected by a spring
Replies
20
Views
640
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
Classical mechanics:effective spring const
Replies
9
Views
3K
Find spring constant k using an electrical circuit
Replies
10
Views
2K
What is the Relationship Between Force and Spring Constant?
Replies
14
Views
3K
Solving Hooke's Law Problems: Compression & Forces
Replies
4
Views
3K
Springs in series and in parallel
Replies
3
Views
2K
Multiple choice Q: Mangetic fields and Spring Constant
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top