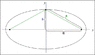
To determine the orientation of an ellipse in standard form, if the denominator associated with x is less than that of y, the ellipse is vertical; otherwise, it is horizontal. The semi-major axis (a) is the square root of the larger denominator, while the semi-minor axis (b) is the square root of the smaller denominator. The coordinates of the center are given by (h,k), and the foci lie along the major axis, with coordinates dependent on the ellipse's orientation. The distance from the center to each focus can be calculated using the Pythagorean theorem, where c is the linear eccentricity, derived from the equation a² = b² + c². Understanding these relationships allows for accurate identification of the ellipse's key features, including vertices and foci.