How Do You Find the Effective Resistance Between Points A and B?

  • Thread starter Thread starter zorro
  • Start date Start date
  • Tags Tags
    Resistance
zorro
Messages
1,378
Reaction score
0

Homework Statement


Find the effective resistance between the points A and B.


The Attempt at a Solution



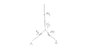
The circuit is a hexagon as shown in the image.
I used star-delta method to convert upper and lower deltas respectively into Ys and then did some simplification. However, I'm stuck up at one place. Refer the two figures.
Please help.
 

Attachments

  • res.jpg
    res.jpg
    6.6 KB · Views: 374
  • ELEC.jpg
    ELEC.jpg
    5.8 KB · Views: 399
Physics news on Phys.org
I think you over-think it. Notice that the circuit is shorted at 3 points M, N and P. Simplify the circuit and it comes down to a simple problem :biggrin:
 

Attachments

  • untitled.JPG
    untitled.JPG
    12.6 KB · Views: 346
Oh! yeaah...it is a very simple problem
Thanks!
 

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

Voltage and effective resistance of an infinite lattice of resistors
Replies
2
Views
2K
How to find the equivalent resistance of this infinite circuit?
Replies
10
Views
2K
Calculating Copper Wire Gauge for Resistance Thermometer Bridge Circuit
Replies
6
Views
2K
I How to understand experiment to measure heat capacity of solid?
Replies
1
Views
2K
How to determine if electrical components are connected in parallel or in series?
Replies
10
Views
966
Effective Resistance between 2 points
Replies
26
Views
3K
How does mirror symmetry for resistance work?
Replies
7
Views
1K
How to Find the Magnetic Field (B) in a Zeeman Effect
Replies
3
Views
1K
Mutual Thermal Resistances between Pipe Layers
Replies
3
Views
1K
What Is the Effective Resistance Between A and F?
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top