Static equilibrium against a wall

[robertmatthew]

Homework Statement

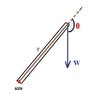
A uniform strut of length, L and weight 780 N is free to pivot about point P where it is attached to the wall (see diagram) A weight W = 815 N hangs straight down from the end of the strut. A rope is attached to the same end as the load and the wall completes the support as shown. Determine the tension in the rope.

Homework Equations

ƩF = 0
Ʃτ = 0

The Attempt at a Solution

0 = τ₁ + τ₂ + τ₃
0 = LTsin90 - (L/2)(sin60)(W₁) - W₂
divide out L's and move weights over
Tsin90 = (1/2)(sin60)(W₁) + W₂
T = (1/2)(sin60)(W₁) + W₂
plug in weights and solve
T = 1152.7499 N

Which isn't right. I don't really know where I'm going wrong, I've tried a few different things but they're not working. I can solve these when beam is horizontal, so I'm guessing my error has something to do with what I'm doing with the angles.

 

[TSny]

0 = τ₁ + τ₂ + τ₃
0 = LTsin90 - (L/2)(sin60)(W₁) - W₂

Do you have the right trig factor here? Shouldn't the last term also have a trig factor as well as a factor depending on L?

 

[robertmatthew]

Whoops, that should have been 0 = LTsin90 - (L/2)(sin60)(W1) - LW2, right? But I can't figure out which trig factors I should be using.

 

[MrSelfDestruct]

Whoops, that should have been 0 = LTsin90 - (L/2)(sin60)(W1) - LW2, right? But I can't figure out which trig factors I should be using.

I would recommend you choose your coordinate axis carefully, something like having the y-axis pass right through the beam and the x-axis being perpendicular to the bar. It will help you with the trig because now you will be able to visualize the components and Trig clearer. If you can visualize this then you will be able to figure out how do it for when you had the original coordinate axis setup, which I am assuming was flush with the wall.

Since you choose to solve using summation of moments the equation should look like

(+)CCW Direction Sum: 0 = -(L/2)F1sin30 + LT - LF2sin30

With T= 1083N

 

[robertmatthew]

I tried that T value but it wasn't the right answer.

 

[TSny]

We need to find out why you are having trouble with determining the correct trig expression. Can you explain how to find the torque of a force about an axis?

 

[robertmatthew]

Isn't it torque = rFsinθ?

 

[TSny]

OK, but can you explain how to find θ?

 

[robertmatthew]

I would assume it's just the angle between r and F, but I'm recalling something about it actually being the angle supplementary to that, or something along those lines?

 

[TSny]

If you consult your text or notes, you should find that the angle is the angle between r and F, as you first guessed. For example, see the attached picture. You often need to extend r as shown by the dotted line. Can you figure out what θ is for the weight hanging at the end of the strut?

 

[robertmatthew]

Is it 30°?

 

[TSny]

Nor sure how you got that. See the attached figure.

 

[robertmatthew]

Oh, I had used the angle supplementary to that by just looking at the beam and the smaller angle between it and the weight. So that would be 150, right? Because the angle of elevation of the beam is 60 and the the third angle of the beam-horizontal-weight triangle is 30, so the angle of the extended r to the weight is 150?

 

[TSny]

Yes, that's correct. Now, it turns out that supplementary angles have the same sine. So, sin30 = sin150 and you would be ok using sin30.

 

[robertmatthew]

So would it then be:

0 = LTsin90 - (L/2)(sin60)(W₁) - L(sin30)W₂

 

[TSny]

So would it then be:

0 = LTsin90 - (L/2)(sin60)(W₁) - L(sin30)W₂

Go through the same procedure to find the correct angle for W₁.

 

[robertmatthew]

Would it also be 150, because if a line is drawn from the center of mass down to be perpendicular to the horizontal, it would be parallel to the rope W₂ is hanging from, right? And therefore its angles to the beam are the same?

 

[TSny]

Yes, that's right. Good.

 

[robertmatthew]

I only have two more attempts in WebAssign, so I just want to make sure I have this right before I plug things in. Would this be correct then?
0 = LTsin90 - (L/2)(sin30)(W1) - L(sin30)(W2)

 

[TSny]

Looks good.

 

[robertmatthew]

Yep, got the right answer. Thank you!