jklops686
- 39
- 0
Homework Statement
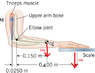
The forearm weighs 20.0 N and has a center of gravity in the position shown in the diagram. The person is pushing DOWN on the weight scale shown in the picture. If the reading on the scale is 70 N, calculate the tension, M, in the triceps muscle.
I understand how this problem works. My question is with the FBD, and which way the force vectors are supposed to go. My intuition (like in my attachment pic) is that the hand pressing on the scale would be going down (counterclockwise negative direction). But there should also be the reaction force going up? I've talked to people and it seems the correct answer should be with the arrow going up in order to get a positive answer for M.
Homework Equations
M=0
The Attempt at a Solution
What makes sense to me:
-70(0.4)-20(.15)-M(.025)=0 So, M=-1240
What I think the answer is:
70(0.4)-20(.15)-M(.025)=0 So, M=+1000
So why won't there be a down force from the hand pushing down?