- #1
gigli
- 11
- 0
Homework Statement
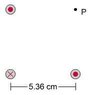
Three parallel wires are arranged in a partial square configuration with point P as the fourth corner. In two of the wires at opposite corners of the square, a 5.00×10^-4 A current flows toward you, and in the third wire opposite the point P, a 7.50×10−4 A current flows away from you. The sides of the square are 5.36cm. What is the strength of the magnetic field at the point P, at the "missing corner" of the square? (T)
Homework Equations
I believe I should be using:
(Magnetic field)=[(Permeability of free space)*(current)]/[2*pi*(distance from wire)]
The permeability of free space = (4*pi*10^-7)
The Attempt at a Solution
B1+B2-B3=BP
[(5E-4)((4*pi)E-7)]/(2*pi*.0536) = B1 = B2 = 1.9788436E-9 T
distance from wire3 and point P = r = sqrt(.0536^2+.0536^2) = .0758018469 m
[(7.5E-4)((4*pi)E-7)]/(2*pi*r) = B3 = 1.97884361E-9 T
So, B1+B2-B3 = 1.752E-9 T
which is not correct unfortunately. Do the parallel wires do something weird I am unaware of? I thought only the distance from the wire and the current determined the magnitude of the magnetic field, and the opposing currents caused opposing magnetic fields. Help!
Attachments
Last edited: