Stress-Strain of Alloy with 100μm Nucleus Size

[Dell]

as depicted in the diagram below

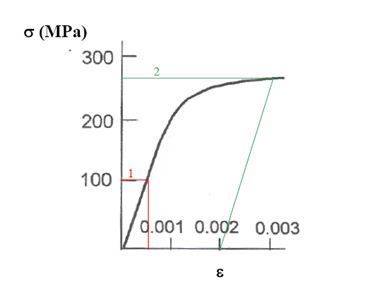
the stress strain for an alloy with an average nucleus size of 100 micron
find
1)the modulus of elasticity for the alloy
2) the yielding stress


for 1) i assume that the red line is meant to be at 0.0005 therefore
E=dσ/dε=100e6/0.0005

E=200Gpa

for 2) i don't know what i can do, all that i do know is that the slant of the line from ε=0.002 to the point of σ_y is equal to 200Gpa (from the E i found before), but how can i use this to find the stress, i do not know the strain for σ_y, since i was given the nuclesu size i think i must somehow use that, but how??

 

[chemisttree]

Ignore the 100 micron nucleus info. The sample yields where there is a deviation from a linear stress/strain relationship, right?

 

[Dell]

but how can i use that information, when you say a deviation from stress strain relationship, do you mean a deviation from the young modulus? i don't think that that's true, is there not a small portion where the line is not linear but before yielding?
even on the graph there is a portion between the linear section and the point marked as 2 with the green line

 

[Dell]

i think i need to use the imaginary linear line that starts at 0.2% and rises to yielding stress at a slant equal to E

 

[Mapes]

Agreed.

 

[Dell]

now i assume that the apropriate strain for the yielding stress is 0.003, is that correct?

σ/0.001=E=200Gpa

σ=200MPa

is this correct? according to the graph it cannot be

 

[Mapes]

It's simpler than that. The convention is to use the stress where the 0.2% offset line meets the actual stress-strain curve.

 

[Dell]

but i don't know the function of the actual curve, do you mean the linear section,
where
σ=200Gpa*ε
(ε=0.002)

σ=400MPa

dont think that's what you mean,

how can i find the curve after the linear section?

 

[Mapes]

You read it off by eye.

 

[Dell]

is there no way to calculate it?

 

[Dell]

could you please take a look at these posts of mine too
https://www.physicsforums.com/showthread.php?t=361931
https://www.physicsforums.com/showthread.php?t=361935