person123
- 326
- 52
- TL;DR Summary
- I was wondering if the deformation of a bending beam would lead to normal stress perpendicular to the applied stress and if deformation causing stress is common and important to consider.
Hi. Say you apply a moment on a beam and bend it into an arch. If you take a free body diagram of a section of the beam you would need normal stresses in the radial direction to balance the forces:
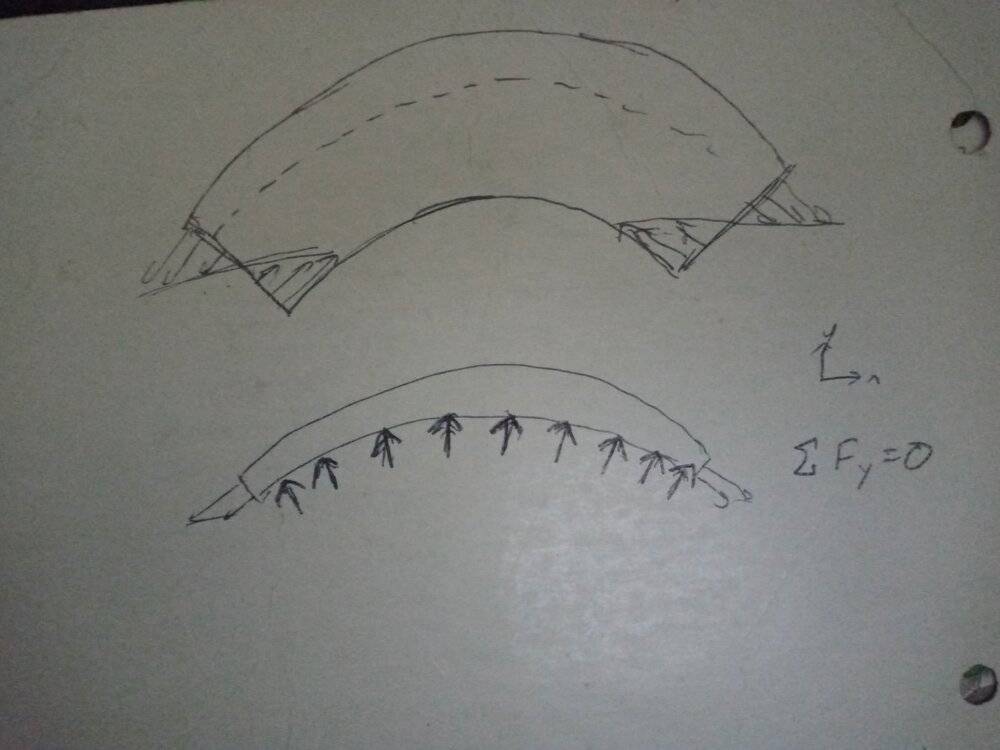
I have never seen this brought up before though -- is it correct logic? Also, is this sort of situation where deformation leads to other stresses common? Thanks!
I have never seen this brought up before though -- is it correct logic? Also, is this sort of situation where deformation leads to other stresses common? Thanks!