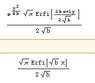- #1
- 4,807
- 32
Yes, it's me and the wave packets... again!
This is taken from the text of Gasiorowicz's Quantum Physics 3rd ed. pp.26.
We have a gaussian wave packet at t=0 that is is described by
[tex]\psi(x,0)=\int_{-\infty}^{\infty}dke^{-\alpha (k-k_0)^2/2}e^{ikx}[/tex]
and we apply the change of variable [itex]q' = k-k_0[/itex]. Suposedly the wave packet becomes
[tex]\psi(x,0)=e^{ik_0x}e^{-x^2/2\alpha}\int_{-\infty}^{\infty}dq'e^{-\alpha q'^2/2}[/tex]
How does one gets to that? When I make the substitution k = q' + k_0, I get
[tex]e^{ik_0x}\int_{-\infty}^{\infty}dq' e^{-\alpha q'^2/2}e^{iq'x}[/tex]
This is taken from the text of Gasiorowicz's Quantum Physics 3rd ed. pp.26.
We have a gaussian wave packet at t=0 that is is described by
[tex]\psi(x,0)=\int_{-\infty}^{\infty}dke^{-\alpha (k-k_0)^2/2}e^{ikx}[/tex]
and we apply the change of variable [itex]q' = k-k_0[/itex]. Suposedly the wave packet becomes
[tex]\psi(x,0)=e^{ik_0x}e^{-x^2/2\alpha}\int_{-\infty}^{\infty}dq'e^{-\alpha q'^2/2}[/tex]
How does one gets to that? When I make the substitution k = q' + k_0, I get
[tex]e^{ik_0x}\int_{-\infty}^{\infty}dq' e^{-\alpha q'^2/2}e^{iq'x}[/tex]