Sum formula for the modified Bessel function

[Hanyu Ye]

Hi, everybody. Mathematic handbooks have given a sum formula for the modified Bessel function of the second kind as follows

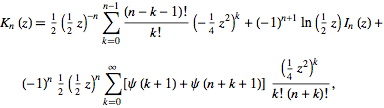
I have tried to evaluate this formula. When z is a real number, it gives a result identical to that computed by the 'besselk ' function in MATLAB. However, when z is a complex number, the two results don't agree. What's wrong? Thanks a lot.

 

[RUber]

Hi Hanyu,
I looked into some other series expansions, and found this one...from wolfram.com. It looks almost exactly like the one you were using above except for the $I_n(z)$ in your post was replaced by another sum formula.

Using this in matlab, I was able to get the same results as besselk for a sample of real and imaginary points.
So...I would look into the requirements for the function $I_n(z)$ that you were using to see if there are complications from the imaginary input.

Below is how I input it into matlab:
[\code]
function A=Kest(n,z);
expand = 10;
sum1 = 0;
for k = 0 :expand
sum1 = sum1 + (z/2)^(2*k)/factorial(k)/factorial(k+n);
end
term1 = (-1)^(n-1)*log(z/2)*(z/2)^n*sum1;

sum2 = 0;
%if n==0
%else
for k = 0:n-1
sum2 = sum2+(-1)^k*factorial(n-k-1)/factorial(k)*(z/2)^(2*k);
end
%end
term2 = sum2*1/2*(z/2)^(-n);

sum3 = 0;
for k = 0 :expand
sum3 = sum3 + (psi(k+1)+psi(k+n+1))/factorial(k)/factorial(k+n)*(z/2)^(2*k);
end
term3 = sum3*(-1)^n/2*(z/2)^n;
A = term1+term2+term3;
[/code]