jessicak
- 24
- 0
Homework Statement
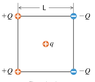
Four point charges of +/-Q are arranged on the corners of a square of side L. What is the net electric force that these charges exert on a point charge q placed on the center of the square (formula in terms of Q, q, L and Coulumb constant k)?
Homework Equations
F=kQq/r^2
The Attempt at a Solution
The four electric forces point in two directions, two to the upper right handed corner and two to the lower right hand corner. These forces are all equal in magnitude because they each have the same magnitude of charge. The y components of these forces cancel, because they are in opposite directions. I also used the Pythagorean theorem to find the distance between charges. That leaves 4 forces equal in magnitude in the positive x direction. Solving for one of these charges gives:
F= (kqQ/0.5L2)cos(45)= 2kqQ/L2cos(45)
I'm then thinking to multiply this by 4, but I'm not getting the correct answer. Any help would be appreciated