- #1
rab99
- 104
- 0
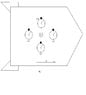
Referring to Fig A
We have a spaceship in the spaceship is an observer at point D.
There is also 4 identical clocks, clock 1 (C1), clock 2 (C2), clock 3 (C3) and clock 4 (C4).
At the same point as the observer is a light so there is a light at point D as well.
The observer also has a stopwatch.
While the spaceship is on the launch pad the observer spaces the clocks so they are all equidistant from the light as measured by the observer. So the distance from D to C3 is the same distance as D to C4 which is the same as the distance D to C2 which is the same as the distance D to C1.
V is the velocity of the spaceship and the arrow denotes it direction. Both V and the direction we will say for now are unknown.
All of the clocks, lights and observers are at rest wrt the space ship.
The observer wants to perform and experiment to determine if he is moving and in what direction.
The observers will synchronise the clocks using the Einstein methods of synchronizing clocks. By emitting a flash of light and the photons from the light synchronises the clocks.
While the spaceship is on the launch pad ie assume V = 0 and direction = 0 the observer synchronises the clocks.
He then walks from clock to clock, clock1 first then clock 2 then clock 3 then clock 4. Using his stop watch he times how long it takes to walk from clock to clock. At each clock he notes the time on the clock and the time on his stop watch.
The times he gets for the four clocks are T1 for Clock 1, T2 for Clock 2, T3 for clock 3 and T4 for clock 4.
The times he gets on his stop watch when walking between D and clock 1 is tD_1
The times he gets on his stop watch when walking between clock 1 and clock 2 is t1_2
The times he gets on his stop watch when walking between clock 2 and clock 3 is t2_3
The times he gets on his stop watch when walking between clock 3 and clock 4 is t3_4
He discovers that all the clocks are synchronised ie T1 = T2 = T3 = T4
He then collects all the clocks together at point D and compares the times on each clock just by looking at them and again he discovers that all the clocks are synchronised ie T1 = T2 = T3 = T4
Then spaceship takes off and accelerates up to a constant velocity V and the observer performs exactly the same experiment as he did above. The observer doesn’t know that he is moving and doesn’t know what V is.
He walks from clock to clock same as above will the clocks be synchronised ie T1 = T2 = T3 = T4?
He then collect all the clocks together at point D and compares the times on each clock just by looking at them will the clocks be synchronised ie T1 = T2 = T3 = T4?
We have a spaceship in the spaceship is an observer at point D.
There is also 4 identical clocks, clock 1 (C1), clock 2 (C2), clock 3 (C3) and clock 4 (C4).
At the same point as the observer is a light so there is a light at point D as well.
The observer also has a stopwatch.
While the spaceship is on the launch pad the observer spaces the clocks so they are all equidistant from the light as measured by the observer. So the distance from D to C3 is the same distance as D to C4 which is the same as the distance D to C2 which is the same as the distance D to C1.
V is the velocity of the spaceship and the arrow denotes it direction. Both V and the direction we will say for now are unknown.
All of the clocks, lights and observers are at rest wrt the space ship.
The observer wants to perform and experiment to determine if he is moving and in what direction.
The observers will synchronise the clocks using the Einstein methods of synchronizing clocks. By emitting a flash of light and the photons from the light synchronises the clocks.
While the spaceship is on the launch pad ie assume V = 0 and direction = 0 the observer synchronises the clocks.
He then walks from clock to clock, clock1 first then clock 2 then clock 3 then clock 4. Using his stop watch he times how long it takes to walk from clock to clock. At each clock he notes the time on the clock and the time on his stop watch.
The times he gets for the four clocks are T1 for Clock 1, T2 for Clock 2, T3 for clock 3 and T4 for clock 4.
The times he gets on his stop watch when walking between D and clock 1 is tD_1
The times he gets on his stop watch when walking between clock 1 and clock 2 is t1_2
The times he gets on his stop watch when walking between clock 2 and clock 3 is t2_3
The times he gets on his stop watch when walking between clock 3 and clock 4 is t3_4
He discovers that all the clocks are synchronised ie T1 = T2 = T3 = T4
He then collects all the clocks together at point D and compares the times on each clock just by looking at them and again he discovers that all the clocks are synchronised ie T1 = T2 = T3 = T4
Then spaceship takes off and accelerates up to a constant velocity V and the observer performs exactly the same experiment as he did above. The observer doesn’t know that he is moving and doesn’t know what V is.
He walks from clock to clock same as above will the clocks be synchronised ie T1 = T2 = T3 = T4?
He then collect all the clocks together at point D and compares the times on each clock just by looking at them will the clocks be synchronised ie T1 = T2 = T3 = T4?