T-Shaped Pendulum: Find the Total Mechanical Energy

[Nate]

Homework Statement

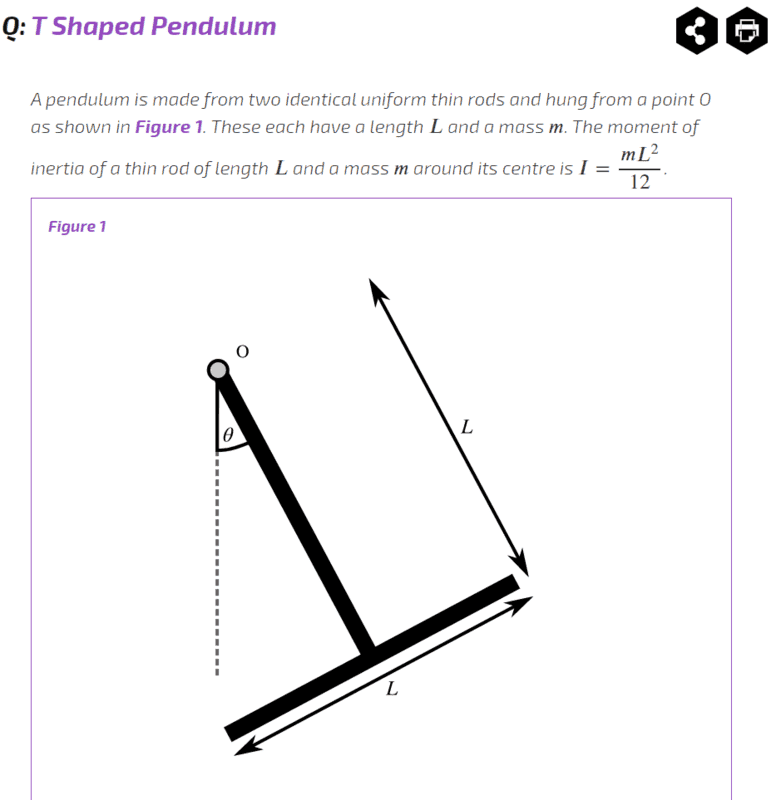
A pendulum is made from two identical uniform thin rods and hung from a point O. These each have a length 𝐿 and a mass 𝑚. The moment of inertia of a thin rod of length 𝐿 and a mass 𝑚 around its centre is 𝐼=𝑚𝐿^2/12.
Part A:Given that 𝐿=31.0cm and 𝑚=100g, what is the moment of inertia of the whole T about the point O?
Part B: What is the potential energy of the pendulum if it is at an angle 𝜃=30.0° to the vertical, if its potential energy is taken to be zero at 𝜃=0°?
Part C: By working out the total energy when the pendulum is in motion, and remembering that this must remain constant, or by using the angular equivalent of Newton's Second Law, find the period of small oscillations of the pendulum.

Relevant Equations

For Part A a relevant equation is the parallel axis theorem, I=I𝖢𝗈𝖬+𝑚l^2
For Part B a relevant equation is potential energy (PE)=mgh
For Part C a relevant equation for simple harmonic motion is ¨x =−𝜔^2x

My answer to part A is correct but for Part B I got an incorrect answer of 0.204J. My working out is sent as an attachment.

Part A:

Part B:

Part C:

 

[Doc Al]

Putting your work in an attachment makes it difficult to comment on. In the future, type up your work right here.

You found the location of the center of mass. Compare the initial and final positions of that center of mass. (I don't see where you got the equation you used for "h".)

 

[Nate]

Hi Doc Al, Thank you for your comment, I appreciate this! I just worked out Part B! I made an error for the "h" equation. Since h=l(1-cosθ) and the position of the centre of mass from the point O is l/4 then the position of the centre of mass from the pivot is 3l/4. Therefore the potential energy is 3/4x0.31x2x0.1x9.81x(1-cos30)=0.0611J(3sf). This is the correct answer for Part B. I am not sure what the outcome would be if I compare the initial and final positions of the centre of mass?

 

[Nate]

Hi Doc Al, I just finished solving the whole problem, the time period of the pendulum is 1.09s(3sf).

 

[Doc Al]

I am not sure what the outcome would be if I compare the initial and final positions of the centre of mass?

You might not realize it, but that's exactly what you calculated.

To calculate the change in potential energy you must calculate how high the center of mass raises from its initial position. That's what "h" is. (And you did it.)

 

[Nate]

Oh, that's true! Thank you!

 

[PraneethL]

Hi Doc Al, I just finished solving the whole problem, the time period of the pendulum is 1.09s(3sf).

Hey, would you mind working me through how you got that? I am a bit stuck

 

[kuruman]

Hey, would you mind working me through how you got that? I am a bit stuck

This thread is more than a 3 years old and @Nate has not been seen here in more than 2 years. Chances are you will not get answer from him any time soon. I suggest that you post your question on a separate homework thread.

Since you are new here, please read, understand and follow our homework guidelines, especially item 4, here
https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

 

[berkeman]

Hey, would you mind working me through how you got that? I am a bit stuck

Welcome to PF.

As mentioned, please start a new thread in these schoolwork forums and show your work on the solution. You will get great help here as long as you show your work Thank you.

This thread is now closed.