Tension in a flexible circular loop

[cheapstrike]

Homework Statement

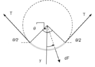
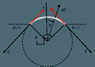
A small circular flexible loop of wire of radius R carries a current I. It is placed in a uniform magnetic field B. The tension in the loop will be double if

A) I is doubled B) B is halved C) r is doubled D) both B and I are doubled.

Homework Equations

The Attempt at a Solution

(Assuming B to be inside plane of paper and I to be clockwise)
The way I am looking at the problem is that because the loop is flexible its area will increase and because of the increase in area that total flux passing through the loop will also increase. This change in flux will induce an EMF which leads to an anticlockwise current, thereby reducing net current.
I think we then have to find a relation between I and r but I can't understand how to do it.
I don't even know if this is correct way to approach.
Please help.

 

[kuruman]

What is the relevant equation showing where the tension comes from?

 

[cheapstrike]

What is the relevant equation showing where the tension comes from?

I think F=I(lxB) where l will be 2*pi*r?

 

[kuruman]

I think F=I(lxB) where l will be 2*pi*r?

No. Consider first an element dl = r dθ and the force acting on it at each of its ends.

 

[cheapstrike]

No. Consider first an element dl = r dθ and the force acting on it at each of its ends.

Will the force acting on the dl element not be radially outwards?

 

[kuruman]

It will indeed be radially outwards, but the rest of the loop will keep it in place by exerting tension at its ends. Draw a FBD.

 

[cheapstrike]

It will indeed be radially outwards, but the rest of the loop will keep it in place by exerting tension at its ends. Draw a FBD.

Ok.. so in the FBD, there will be an outward force and a force on both sides of dl due to the other two ends. But can we get any relation from here?
I mean the loop is elastic so won't it expand?

 

[kuruman]

mean the loop is elastic so won't it expand?

According to the problem, the wire is flexible not elastic and its radius is fixed at R. I don't interpret this as meaning that the loop can stretch. All it means is that it wll assume a circular shape of radius R.

 

[cheapstrike]

According to the problem, the wire is flexible not elastic and its radius is fixed at R. I don't interpret this as meaning that the loop can stretch. All it means is that it wll assume a circular shape of radius R.

Ah.. I got mixed up with that. Ok. So the element dl will remain at it's place meaning net force on it is zero? So, the net outward force = I(dlxB) will be balanced by the two forces at it's ends. Btw how will we do it?

 

[cheapstrike]

According to the problem, the wire is flexible not elastic and its radius is fixed at R. I don't interpret this as meaning that the loop can stretch. All it means is that it wll assume a circular shape of radius R.

I think the force acting radially outwards on the element dl will be I(dlxB) which is IdlB as dl is perpendicular to B. This force will be balanced by sin of both the tension forces. Also, their cosines will cancel each other.
So we will have an equation IdlB=2Tsin(dx), where T is the tensional force and dx is the angle which each tension vector makes with the tangent at dl (dx is d(theta)). As dx is small, sin(dx)=dx.
So equation becomes IdlB=2Tdx
Giving T=IdlB/2dx.
dl/dx can be written as r where r is the radius.
So, T=IBr/2.
But this seems incorrect to me as, in this case, T will be doubled on doubling I as well as r.
But I believe the question is single correct (I don't know the answer but I think it's single correct).
Can you please tell what is wrong with this and also the correct equations.
Thanks.

 

[kuruman]

It looks like your tension is half of what it ought to be. Here is the FBD. You need to balance forces in the y-direction. Remember to integrate the y-component of dF using integration variable φ.

 

[cheapstrike]

It looks like your tension is half of what it ought to be. Here is the FBD. You need to balance forces in the y-direction. Remember to integrate the y-component of dF using integration variable φ.

View attachment 115625

Ok.. so I took the angle that T vector makes incorrectly. It should be dx/2.

 

[kuruman]

Can you finish now?

 

[cheapstrike]

It looks like your tension is half of what it ought to be. Here is the FBD. You need to balance forces in the y-direction. Remember to integrate the y-component of dF using integration variable φ.

View attachment 115625

I am a little unsure about this but, I wrote this as
dFcosφ=Tθ (i wrote sinθ=θ) and then wrote dF as IdlB where dl is rdφ and integrated it from -θ/2 to θ/2 and wrote sinθ/2=θ/2 and finally got
IBr=T.
Is this correct?
If this is, then shouldn't the answer be A) and C)?

 

[kuruman]

IBr=T.

That's what I got.

If this is, then shouldn't the answer be A) and C)?

I would say the answer is A or C. Are you sure this is not a multiple answer question?

 

[cheapstrike]

That's what I got.

I would say the answer is A or C. Are you sure this is not a multiple answer question?

I am not sure, i don't even know the answer. But the method seems correct.. :D
Thanks a lot

 

[haruspex]

shouldn't the answer be A) and C)?

I would say the answer is A or C

English is not great for expressing logical predicates.
The tension will double if A or C is done; the tension will double if A is done and the tension will double if C is done.

 

[kuruman]

... the tension will double if A is done and the tension will double if C is done.

Exactly why this should be put forth as a "multiple answer" question where A and C are the two correct answers. It cannot be a "multiple choice" question which guarantees that only one answer is correct and which can be answered either by proving/deriving the correct answer or by showing that each of the n - 1 answers is incorrect.

Here, the statement "the tension will double" is true if either A is true or C is true, but not if both are true. Perhaps I should have written, "I would say the answer is A xor C" in an effort to remedy the shortcomings of the English language with logic.

 

[cheapstrike]

There is no point in writing this but...
I think, saying A and C are correct is fine coz these two are two different cases. In A) only I is being doubled and in C) only r is being doubled. That's why option D) is there which shows that if the asker of the question wants to change two parameters in 1 case together, he must mention them together under a single option.

As far as this question is considered, either there is a printing mistake or it's a multiple correct. I think it's former coz question claimed to be single correct.

 

[Piyushagg]

You all r putting a lot of brain...it has now formed a closed loop so F=mxB
m=(pi*r*r)*i
This implies on increasing current i or magnetic field B...Force will double.
In ur case it is "on incresing current". Hope it was correct.

 

[kuruman]

You all r putting a lot of brain...it has now formed a closed loop so F=mxB

You r incorrect. Torque, not force is mxB. We are concerned with force here.

 

[Piyushagg]

I was thinking that net force is suppose to be zero in a closed loop in uniform magnetic field but torque is mostly non zero so if torque increases then force increases that's what i thought, sorry for putting it in that way, get me corrected if i am wrong again. any kind of help is appreciated.

 

[kuruman]

I was thinking that net force is suppose to be zero in a closed loop in uniform magnetic field but torque is mostly non zero so if torque increases then force increases that's what i thought, sorry for putting it in that way, get me corrected if i am wrong again. any kind of help is appreciated.

You are correct in saying that the net force is zero in this case, but you misunderstood the question. If you place a flexible limp loop in a uniform magnetic field and run a current through it, equilibrium will be reached when the loop forms a circle with its plane perpendicular to the magnetic field. In this configuration the net torque and the net force on the loop will be zero. However, each arc segment ds on the loop will experience a magnetic force I ds B directed radially out. This will put the wire loop under tension T which is what this question is about.

 

[haruspex]

equilibrium will be reached when the loop forms a circle with its plane perpendicular to the magnetic field

Right, but I note this in the OP:

Assuming B to be inside plane of paper

which seems to be saying the field is perpendicular to the axis of the loop. I assume the OP is wrong on that.

 

[kuruman]

I assume the OP is wrong on that.

I would assume so too. OP mentions next

The way I am looking at the problem is that because the loop is flexible its area will increase and because of the increase in area that total flux passing through the loop will also increase.

If OP is considering flux through the loop then we have a contradiction.

 

[cheapstrike]

I would assume so too. OP mentions next

If OP is considering flux through the loop then we have a contradiction.

Yeah, I mixed up between flexible and elastic. I at first thought that the loop will go on increasing in radius, causing change in flux, till the net current becomes zero.

 

[haruspex]

Yeah, I mixed up between flexible and elastic. I at first thought that the loop will go on increasing in radius, causing change in flux, till the net current becomes zero.

Sure, but there was another mix-up. You wrote that you assumed "B to be inside plane of paper", i.e. the field is parallel to the plane of the loop. I think it is clear that the field is perpendicular to that plane, i.e. parallel to the axis of the loop.

 

[cheapstrike]

Sure, but there was another mix-up. You wrote that you assumed "B to be inside plane of paper", i.e. the field is parallel to the plane of the loop. I think it is clear that the field is perpendicular to that plane, i.e. parallel to the axis of the loop.

Wait.. lol
I also assumed the loop to be in the plane of paper with its axis perpendicular to the plane of paper and B parallel to the axis of the loop. Like generally we draw a loop on paper and take B inside it's plane (x).

 

[haruspex]

I also assumed the loop to be in the plane of paper with its axis perpendicular to the plane of paper

Yes, i assumed you were taking the loop to lie in the plane of the page.

and B parallel to the axis of the loop.

Yes, I believe that is the set-up in this question.

generally we draw a loop on paper and take B inside it's plane (x).

That's different. That says the field is parallel to the page. Do you mean into the page?

 

[cheapstrike]

Yes, i assumed you were taking the loop to lie in the plane of the page.

Yes, I believe that is the set-up in this question.

That's different. That says the field is parallel to the page. Do you mean into the page?

Yes, into :D

 

[Jahnavi]

@haruspex , @kuruman If the current flows in anticlockwise direction (instead of clockwise as in the OP ) and magnetic field is perpendicular to the plane of the page , the direction of force on any infinitesimal portion of the wire will be radially inwards .

Would the force on this tiny element from the neighbouring wire element be exactly opposite to the one shown in post#11 ?

But this force doesn't look like some tension force . Is it some type of compressive force ?

But magnitude of this force will still be BIR just as in the OP .Right ?

 

[haruspex]

But this force doesn't look like some tension force . Is it some type of compressive force ?

But magnitude of this force will still be BIR just as in the OP .Right ?

Yes.

 

[Jahnavi]

Would the force on this tiny element from the neighbouring wire element be exactly opposite to the one shown in post#11 ?

@haruspex ,please reply this .Is the direction of force from the neighbouring elements exactly opposite to the one shown in the diagram in post#11 ?

 

[kuruman]

Yes, it will be opposite. If $d\vec F = I d\vec l \times \vec B$, then $I d (-\vec l) \times \vec B = -d \vec F$.

 

[Jahnavi]

I am not asking about the direction of force on the tiny wire element by the magnetic field

I am asking about the direction of force on the infinitesimal length element from the neighbouring elements . Just like in post#11 you showed the two forces by $T$ .

My question is that if an anticlockwise current flows then the direction of force would be exactly opposite to the one showed by two $T$'s in post#11 ?

 

[kuruman]

The tensions will change direction, if that's what you are thinking. The endpoints of the circuit are assumed fixed so that one can analyze the forces. When the current changes direction, the magnetic force will change direction and you will have the same force diagram as in post #11 except that will be reflected 180^o about the horizontal axis passing through the endpoints (dashed line in post ##11). In other words, the tensions will reverse their perpendicular components to the dashed line, but not their parallel components. In the end, the entire loop will still be under tension except "upside down" in a sense.

 

[Jahnavi]

but not their parallel components.

Please reconsider this .

I think when the current is reversed , both the perpendicular and parallel components should be reversed .

If parallel component is not reversed (as in post#11 ) then the force at the end points of the tiny element will not be tangential .

 

[kuruman]

... you will have the same force diagram as in post #11 except that will be reflected 180^o about the horizontal axis passing through the endpoints ...

Perhaps I wasn't very clear with this statement. The entire diagram will be reflected. This means that the arc under consideration will curve down instead of up.

 

[Charles Link]

@haruspex , @kuruman If the current flows in anticlockwise direction (instead of clockwise as in the OP ) and magnetic field is perpendicular to the plane of the page , the direction of force on any infinitesimal portion of the wire will be radially inwards .

Would the force on this tiny element from the neighbouring wire element be exactly opposite to the one shown in post#11 ?

But this force doesn't look like some tension force . Is it some type of compressive force ?

But magnitude of this force will still be BIR just as in the OP .Right ?

I believe @Jahnavi has it correct. If $\vec{B}$ is upward and $I$ is counterclockwise the force points outward from each part of the loop. $\\$ If the current is clockwise the force from each part of the loop will be of a compressive form, and it will be towards the center of the loop for each part of the loop.

 

[Jahnavi]

If $\vec{B}$ is upward and $I$ is counterclockwise the force points outward from each part of the loop.

No .

I think if the magnetic field is perpendicular to the plane of the page (going in) and current is anticlockwise then force due to magnetic field will be towards the center .The net compressive force on an infinitesimal element should be radially outward .

 

[kuruman]

I believe @Jahnavi has it correct. If $\vec{B}$ is upward and $I$ is counterclockwise the force points outward from each part of the loop. $\\$ If the current is clockwise the force from each part of the loop will be of a compressive form, and it will be towards the center of the loop for each part of the loop.

Minor correction, the magnetic field is perpendicular to the screen. Anyway, yes the force will be compressive, but consider this: imagine a supple segment of a wire tied at both ends such that the distance between the anchor points is less than the length of the wire. Place it in a uniform magnetic field and run a current through it. When the current runs "left to right" the wire will flex and be taut in one direction and if you run the current "right to left" it will be taut and flex in the opposite direction. If you have a closed loop of supple wire all crumpled up and somehow manage to run a current through it, it will stretch and be under tension as long as the current is running. If you reverse the current, yes it will crumple up but it will not stay crumpled up. It will stretch and be under tension again.

 

[Charles Link]

No .

I think if the magnetic field is perpendicular to the plane of the page (going in) and current is anticlockwise then force due to magnetic field will be towards the center .The net compressive force on an infinitesimal element should be radially outward .

The description of my coordinate system needs a little more detail. By "up" (for the magnetic field) I mean positive $z$, and counterclockwise refers to the direction of the current in the x-y plane as viewed from above.

 

[Jahnavi]

Perhaps I wasn't very clear with this statement. The entire diagram will be reflected. This means that the arc under consideration will curve down instead of up.

View attachment 224767

I feel this diagram is same as the one in post#11 .

Please see this .

Don't you think if the current is in anticlockwise direction , direction of force due to neighbouring current wire element will be as shown by the red vectors ?

 

[Charles Link]

@Jahnavi Did you see post 41 by @kuruman ? I think he has concurred that it is compressive for the other case.

 

[Jahnavi]

Yes . I have seen post 41 .

Please clarify , is the direction of force (red vectors ) in the above picture correct ?

 

[Charles Link]

Yes . I have seen post 41 .

Please clarify , is the direction of force (red vectors ) in the above picture correct ?

Yes. I agree with it. We need to see if @kuruman agrees. $\\$ Edit: If this is a loose loop of wire resting on a surface, it would have a tendency to flip over, i.e. compress itself and then expand again with the current running the other way, so that the magnetic moment from the loop of wire $\vec{\mu}=I \vec{A}$ was aligned with the magnetic field, because energy $E=-\vec{\mu} \cdot \vec{B}$. The system would tend to go to the state of lowest energy.

 

[kuruman]

Yes. I agree with it. We need to see if @kuruman agrees. $\\$ Edit: If this is a loose loop of wire resting on a surface, it would have a tendency to flip over, i.e. compress itself and then expand again with the current running the other way, so that the magnetic moment from the loop of wire $\vec{\mu}=I \vec{A}$ was aligned with the magnetic field, because energy $E=-\vec{\mu} \cdot \vec{B}$. The system would tend to go to the state of lowest energy.

I wholly agree with the "Edit" statements by @Charles Link. My arguments rely on the wire being supple as state in post #41. By "supple" I mean "extremely flexible". Consider what will happen to two identical circuits placed in a uniform magnetic field perpendicular to the screen (see below) with currents running in opposite directions. To minimize the energy, one of the two subloops in each circuit will flip over and the the circuit will be under tension and form a circle with the current running in the same direction.

If the circuits are made of very stiff wire but free to rotate, then the subloop with highest magnitude of magnetic moment (here the bottom subloop) will determine the final configuration.

And if the stiff wire circuits are sandwiched between two pieces of stiff plastic, then they will stay as they are with one subloop under tension and the other under compression in each.