alexas
- 52
- 0
Homework Statement
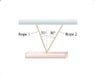
A 1400 kg steel beam is supported by two ropes.
Homework Equations
Tx = mgsin(ANGLE) ?
Ty = mgcos(ANGLE) ??
g = 9.8?
Tension of one wire = [((Tx)^2) + ((Ty)^2)]^(1/2) ?
The Attempt at a Solution
I wasn't too sure whether or not i should use the angle: 20 or 70.So i did it both ways they were both wrong, but i did it both ways...
[((1400(9.8)sin(20))^2) + ((1400(9.8)cos(20))^2)]&(1/2)
And then i did:
[((1400(9.8)sin(70))^2) + ((1400(9.8)cos(70))^2)]&(1/2)
Am i approaching this problem correctly? I have a test Thursday and i feel pretty F***** right now. Any help would be appreciated.