Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Paul E. Bland's book "Rings and Their Modules ...
Currently I am focused on Section 2.3 Tensor Products of Modules ... ...
I need some help in order to fully understand the Remark that Bland makes on Pages 65- 66
Bland's remark reads as follows:
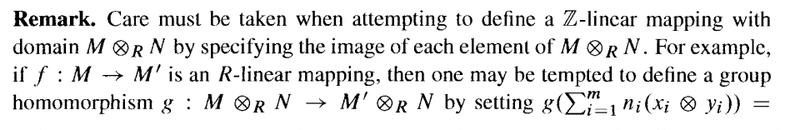

Question 1
In the above text by Bland we read the following:
"... ... but when ##g## is specified in this manner it is difficult to show that it is well defined ... ... "
What does Bland mean by showing ##g## is well defined and why would this be difficult ... ...Question 2
In the above text by Bland we read the following:
"... ... Since the map ##h = \rho' ( f \times id_N )## is an R-balanced map ... ... "Why is ##]h = \rho' ( f \times id_N )## an R-balanced map ... can someone please demonstrate that this is the case?
Hope someone can help ... ...
Peter
=============================================================================The following text including some relevant definitions may be useful to readers not familiar with Bland's textbook... note in particular the R-module in Bland's text means right R-module ...

Currently I am focused on Section 2.3 Tensor Products of Modules ... ...
I need some help in order to fully understand the Remark that Bland makes on Pages 65- 66
Bland's remark reads as follows:
Question 1
In the above text by Bland we read the following:
"... ... but when ##g## is specified in this manner it is difficult to show that it is well defined ... ... "
What does Bland mean by showing ##g## is well defined and why would this be difficult ... ...Question 2
In the above text by Bland we read the following:
"... ... Since the map ##h = \rho' ( f \times id_N )## is an R-balanced map ... ... "Why is ##]h = \rho' ( f \times id_N )## an R-balanced map ... can someone please demonstrate that this is the case?
Hope someone can help ... ...
Peter
=============================================================================The following text including some relevant definitions may be useful to readers not familiar with Bland's textbook... note in particular the R-module in Bland's text means right R-module ...
Attachments
Last edited:

