Rawl
- 2
- 0
Homework Statement
https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/72/72755-bc8e4b32405460abcfa2d8e4880f7037.jpg
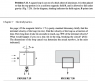
I'm trying to figure out the terminal velocity of the loop as it falls through the magnetic field (figure 7.20).
3. The Attempt at a Solution
The terminal velocity will happen when
\vec{F} = 0
i.e.
mg = \vec{f}_{mag}
But we know:
\oint \vec{f}_{mag} . d\vec{l} = vBl
So
\vec{f}_{mag} = vB
v_t = \frac{mg}{B}
Why is this wrong?
Attachments
Last edited by a moderator: