WorldOfPhysics
- 11
- 0
Dear experts,
when a a stone at the end of the string is rotated with a high speed so that the string is suspended making zero degrees with the plane of the ground, how do we analyze the system from the rotating frame.
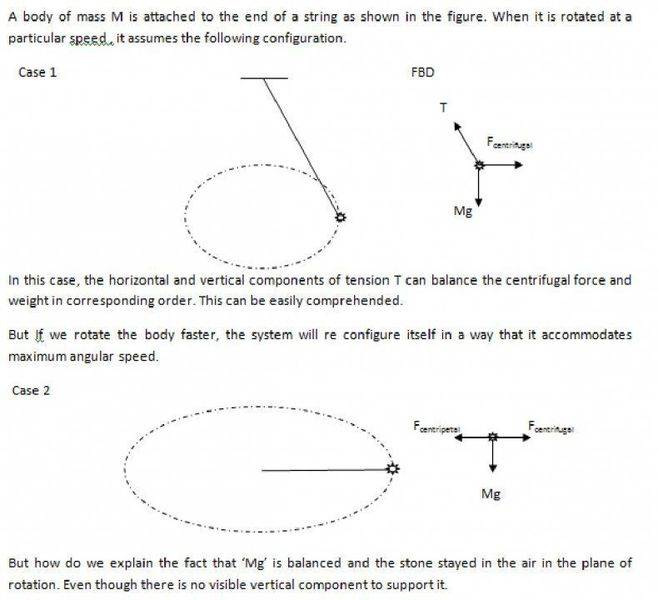
when a a stone at the end of the string is rotated with a high speed so that the string is suspended making zero degrees with the plane of the ground, how do we analyze the system from the rotating frame.
Last edited: