R A V E N
- 63
- 0
- Homework Statement
- How equation ##\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2## is obtained?
- Relevant Equations
- $$\frac{r_1^2}{r_2^2}=k^2=\frac{(d-x)^2+y^2}{x^2+y^2}$$
$$\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2$$
We have a system of two unequal oppositely charged point charges, of which ##q_2## is smaller and ##d## is the distance between charges. There is an equipotential spherical surface of potential ##V=0## that encloses a charge of lesser absolute value. The task is to find parameters of that spherical surface, or more precisely circle, since the system is of course illustrated in two dimensions.
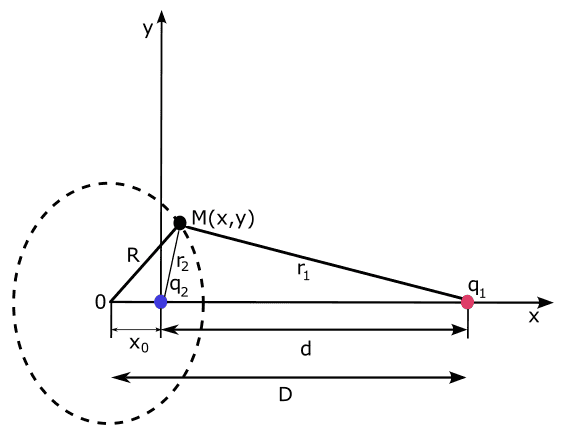 First we take into consideration arbitrary point ##M(x,y)## where ##V=\frac{1}{4\pi\epsilon}\left(\frac{q_1}{r_1}+\frac{q_2}{r_2}\right)##. If we use ##V=0## it's easy to obtain ##\frac{r_1}{r_2}=-\frac{q_1}{q_2}=k## where ##k## is coeficcient of proportionality.
First we take into consideration arbitrary point ##M(x,y)## where ##V=\frac{1}{4\pi\epsilon}\left(\frac{q_1}{r_1}+\frac{q_2}{r_2}\right)##. If we use ##V=0## it's easy to obtain ##\frac{r_1}{r_2}=-\frac{q_1}{q_2}=k## where ##k## is coeficcient of proportionality.
From the illustration, we can see that ##r_1^2=(d-x)^2+y^2## and ##r_2^2=x^2+y^2##. Then we have ##\frac{r_1^2}{r_2^2}=k^2=\frac{(d-x)^2+y^2}{x^2+y^2}## from which ##\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2## is obtained. This equation is the equation of a circle shown in the illustration with coordinates of the circle center ##x_0=-\frac{d}{k^2-1}##, (##|x_0|=\frac{d}{k^2-1}##), and ##y_0=0##. The radius of the circle (equipotential sphere) is ##R=\frac{kd}{k^2-1}=k|x_0|##. How the equation ##\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2## is derived?
For ##q_1## we have ##q_1=2Q##
and for ##q_2## we have ##q_2=−Q## which gives ##k=2##, but I don't see how that can help. Also, this problem uses the method of image charges because it comes after the lesson in my textbook where the method of image charges is explained.
From the illustration, we can see that ##r_1^2=(d-x)^2+y^2## and ##r_2^2=x^2+y^2##. Then we have ##\frac{r_1^2}{r_2^2}=k^2=\frac{(d-x)^2+y^2}{x^2+y^2}## from which ##\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2## is obtained. This equation is the equation of a circle shown in the illustration with coordinates of the circle center ##x_0=-\frac{d}{k^2-1}##, (##|x_0|=\frac{d}{k^2-1}##), and ##y_0=0##. The radius of the circle (equipotential sphere) is ##R=\frac{kd}{k^2-1}=k|x_0|##. How the equation ##\left(x+\frac{d}{k^2-1}\right)^2+y^2=\left(\frac{kd}{k^2-1}\right)^2## is derived?
For ##q_1## we have ##q_1=2Q##
and for ##q_2## we have ##q_2=−Q## which gives ##k=2##, but I don't see how that can help. Also, this problem uses the method of image charges because it comes after the lesson in my textbook where the method of image charges is explained.
Attachments
Last edited: