The lowest pressure on the balloon

[Phatossi]

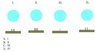
1. Four balloons with the same size are dropped off from the same height on boards that have different numbers of nails. In which of the cases in the balloon will be the lowest pressure?

2. p=F/S
3. I am not sure about the correct answer, but I am saying my opinion about the right answer. By knowing the pressure as the force which acts onto a surface, I am saying that the board with more nails will have the biggest amount of pressure, because there are more nails in the same surface. Please, correct me if I am wrong.

Thank you for your attention.

 

[Doc Al]

Pressure is force per unit area.

Answer this: Which do you think would create greater pressure on the floor: Standing on both feet or standing on one foot?

 

[Phatossi]

Okay, I got it. I am so amazed by the kind of the explanation that you told me, even that it was indirectly, I really understood it. With two feet, you have a lower pressure, in comparison with the pressure that you have staying with one foot.

So, by increasing the numbers of nails on the boards, we have increased the surface of action, in which case we have decreased the pressure. So, I got it. Thank you indeed for your reply.