Zouatine
- 19
- 0
- Homework Statement
- Calcul of stresses
- Relevant Equations
- 1- σ'x=σx*cos(β)^2+σy*sin(β)^2+2*τxy*cos(β)*sin(β)
2- σ'y=σx*sin(β)^2+σy*cos(β)^2-2*τxy*cos(β)*sin(β)
3- τxy'=-σx*sin(β)*cos(β)+σy*sin(β)*cos(β)+τxy*(cos(β)^2-sin(β)^2)
Hi! i have this exercise and solution :
Exercise:
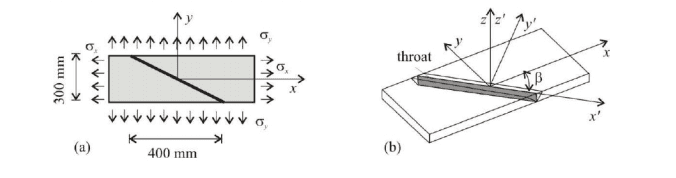
steel plate given in figure (a) is joined by an inclined butt weld ,the plate is subjected to tensile stresses in both x and y directions, σ(x)=54 N/mm^2 and σ(y)=38 N/mm^2 ,
1) Determine the normal and shear stresses of the butt weld.
this is transformation matrices :
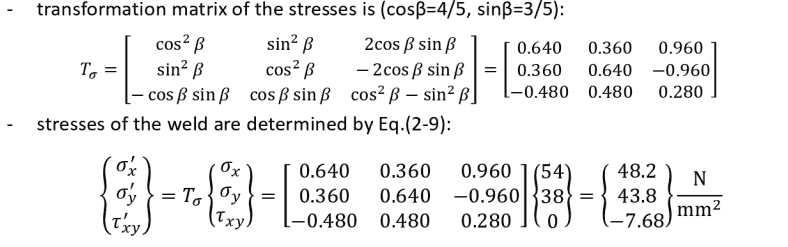
2)second question :
in which direction the stress normal will be maximum ?

My problem: is τxy ( why in first we made it 0 in transformation matrice (and why it's 0) and in second question it's calculed .
Exercise:
steel plate given in figure (a) is joined by an inclined butt weld ,the plate is subjected to tensile stresses in both x and y directions, σ(x)=54 N/mm^2 and σ(y)=38 N/mm^2 ,
1) Determine the normal and shear stresses of the butt weld.
this is transformation matrices :
2)second question :
in which direction the stress normal will be maximum ?
My problem: is τxy ( why in first we made it 0 in transformation matrice (and why it's 0) and in second question it's calculed .