The sums of forces along x and y

[Malitic]

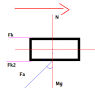
I have a problem I'm working on where the general premise is that there is a box being pushed along the ceiling at a constant speed. The force F is at some angle with respect to the vertical. There is a coefficient of kinetic friction between the box and the ceiling and the persons hands and the box. The latter of which keeps the persons hands from slipping.
I am trying to be deliberately vague because I want help on the concept not the problem itself.

A = angle
$$F_a$$ = Force along the angle A
$$\mu_k$$ = coefficient of friction along the ceiling
$$\mu_{k2}$$ = coefficient of kinetic friction with persons hands
My thinking is that
$$\sum f_x = f_a*sinA - ff = 0 \Rightarrow f_a*cosA = \mu_k*N + \mu_{k2} *N$$
and
$$\sum f_y = f_a*cosA - mg - n = 0$$

Is there a flaw in my logic? Because when I put in all the information my result is unrealistic. I have attached the free body that goes along with my thinking.

 

[Kazza_765]

If the person's hands aren't slipping then ignore the coeffecient of friction between the hands and the box for now.

Now resolve your forces:

In the y direction:
$$F_a*cos(A) - mg - N = 0$$ N is normal reaction between box and ceiling
$$N = F_a*cos(A) - mg$$

In the x direction:
$$F_a*sin(A) - \mu*N = 0$$
$$F_a*sin(A) - \mu(F_a*cos(A) - mg) = 0$$


Now as far as the coeffecient of friction between the hands and the box, this should be a limiting condition.

$$F_a*sin(A) < F_a*cos(A)*\mu$$
$$A < Tan^-1(\mu)$$, so the above equations only hold true if this condition is met.

 

[Malitic]

The force along the x direction in your problem is incorrect because the friction between the box and the hands is important to the problem overall.

However in bug fixing your problem I was able to see where I went wrong so thanks.