PeppaPig
- 25
- 1
Homework Statement
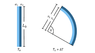
A bimetallic strip is made of metal which has coefficient of thermal expansion is equal to α1 and the other's is equal to α2 at the temperature of T0. The temperature is increased to T0 + ΔT (ΔT > 0). The strip curves as shown in the figure. If both strip have the same width of d. Find r1 measured from the center of the curve to the center of the strip as shown in the figure
Homework Equations
1) radian is (Length of the curve)/(Radius)
2) Using the following estimation
(1 + x)-1 ≈ 1-x and (1 + ax)(1+bx) ≈ 1+(a+b)x for x << 1
The Attempt at a Solution
α1 strip expansion is L0(1 + α1ΔT) for the length
and d(1 + α1ΔT) for the width
α2 strip expansion is L0(1 + α2ΔT) for the length
and d(1 + α2ΔT) for the width
Multiplying radian with radius, the result should be the curve length
r1θ = L0(1 + α1ΔT)
r2θ = L0(1 + α2ΔT)
r2 = r1 + d(2 + α1ΔT + α2ΔT)/2
Is that correct?
Attachments
Last edited: