Thermal Physics: Reversible processes

[WWCY]

Hi all, I have been having some issues trying to show that a reversible expansion of gas does not create new entropy. Assistance is greatly appreciated!

So suppose that a gas expands reversibly as shown below at fixed temperature

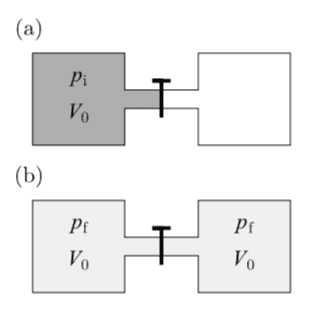
At fixed temperature, internal energy doesn't change so $dU_{sys} = 0$, which means
$$dS_{sys} = \frac{pdV}{T}$$
swapping $p/T$ using the ideal gas law and integrating from $V_0$ to $2V_0$ gives the change in entropy of the system
$$\Delta S_{sys} = nR\ln{2}$$
In my text (Blundell), the authors say that because this reaction has been defined to be reversible, the change in the entropy of the surroundings must be $\Delta S_{su} = \Delta S_{sys}$. I have been trying to show this and have been unsuccessful. What I tried was the following:

Conservation of energy means that $dU_{sys} = -dU_{su} = 0$. The thermodynamic equation for the surrounding is then,
$$T_{su} dS_{su} = p_{su}dV_{su}$$
I supposed, then $T_{su}$ should be equal to $T_{sys}$, since it was not specified that the container was thermally isolated. This left me with
$$dS_{su} = \frac{1}{T}p_{su}dV_{su} = nR\frac{1}{V_{su}}dV_{su}$$
Then it struck me that I had no clue what the "surrounding" actually was. If it refers to the space outside the container, $dV_{surr} = 0$ which means no change in surrounding entropy, which is clearly wrong. If i consider it to be the evacuated space that the gas expands into...it doesn't look right as well.

I know that $dS_{total} = 0$, but due to the fact that identifying what's reversible and what's not is a tricky business for me, I would prefer to work things out explicitly to see if total entropy changes

Could someone point out where I went wrong and how I should have worked this out?

Many thanks!

 

[Chestermiller]

This is not a reversible process. You determined the change in entropy of the system correctly. But the change in entropy of the surroundings is zero. And the change in entropy of the universe is equal to the change in entropy of the system. The entropy generated overall is just that generated in the system.

 

[WWCY]

This is not a reversible process. You determined the change in entropy of the system correctly. But the change in entropy of the surroundings is zero. And the change in entropy of the universe is equal to the change in entropy of the system. The entropy generated overall is just that generated in the system.

Apologies, the diagram was a mistake. What I meant to say was that I was calculating a reversible, isothermic expansion of the gas whereby the tap isn't just suddenly opened, but slowly expanded into the evacuated volume. How would I calculate the entropy of the surroundings in this case?

 

[Chestermiller]

Apologies, the diagram was a mistake. What I meant to say was that I was calculating a reversible, isothermic expansion of the gas whereby the tap isn't just suddenly opened, but slowly expanded into the evacuated volume. How would I calculate the entropy of the surroundings in this case?

It doesn't matter that the gas is slowly expanded into the evacuated volume. The process you describe is still irreversible. Can you think of an alternate reversible process path that would bring the gas to the same final state. Here is a tutorial on how to determine the change in entropy for irreversible processes like this, with a worked example for this specific process: https://www.physicsforums.com/insights/grandpa-chets-entropy-recipe/

 

[WWCY]

It doesn't matter that the gas is slowly expanded into the evacuated volume. The process you describe is still irreversible. Can you think of an alternate reversible process path that would bring the gas to the same final state. Here is a tutorial on how to determine the change in entropy for irreversible processes like this, with a worked example for this specific process: https://www.physicsforums.com/insights/grandpa-chets-entropy-recipe/

That's really puzzling. This was a point made in my text though (eq 14.30), I've attached the relevant passages below in case I misinterpreted it. Also, thank you for the link, I'll give it a read!

 

[Chestermiller]

That's really puzzling. This was a point made in my text though (eq 14.30), I've attached the relevant passages below in case I misinterpreted it. Also, thank you for the link, I'll give it a read!

View attachment 238889
View attachment 238888

I agree with everything in this passage. For the reversible expansion of an ideal gas, the change in entropy of the surroundings is minus the change in entropy of the system. For an irreversible Joule-Thompson expansion, the change in entropy of the gas is the same as that for an irreversible expansion of the gas between the same initial and final states. But, the change in entropy of the surroundings in a Joule-Thompson expansion is zero, since no heat is transferred between the system and surroundings in this case (and so the surroundings experience no change whatsoever).

 

[dRic2]

That's really puzzling. This was a point made in my text though (eq 14.30), I've attached the relevant passages below in case I misinterpreted it. Also, thank you for the link, I'll give it a read!

View attachment 238889
View attachment 238888

I think you misunderstood what the author is saying. Here you have an irreversible process and you want to calculate the change in entropy. Since it is difficult to do this for the irreversible process you imagine an alternative reversible process that has the same initial and final state. But this other process is different from the one you are studying: it serves only like "trick". This "new" process is also reversible by definition (you chose it to be this way) so you do not need to prove anything.

 

[WWCY]

Thanks for the replies.

I am still confused. If we wish to circumvent the calculation of entropy change via an irreversible path, we choose some path whereby quasi-static changes are enacted on the system between the exact same initial and final states, this I think I understand. In both the Joule Expansion and quasi-static expansion the entropy changes within the system are the same, this too I understand. But I have some other questions:

a) Do we conclude that in the Joule expansion, the surrounding sees no change in entropy as $dU_{surr}$ (by conservation of energy) and $dV{surr}$ are both 0?

b) If the quasistatic expansion represents a different physical process, shouldn't it be possible for us to mathematically calculate that the change in entropy is opposite of that produced in the expansion, rather than rely on "definitions"?

Thank you both for being patient.

 

[Chestermiller]

Thanks for the replies.

I am still confused. If we wish to circumvent the calculation of entropy change via an irreversible path, we choose some path whereby quasi-static changes are enacted on the system between the exact same initial and final states, this I think I understand. In both the Joule Expansion and quasi-static expansion the entropy changes within the system are the same, this too I understand. But I have some other questions:

a) Do we conclude that in the Joule expansion, the surrounding sees no change in entropy as $dU_{surr}$ (by conservation of energy) and $dV{surr}$ are both 0?

Yes. This is correct.

b) If the quasistatic expansion represents a different physical process, shouldn't it be possible for us to mathematically calculate that the change in entropy is opposite of that produced in the expansion, rather than rely on "definitions"?

Thank you both for being patient.

I don't quite understand this part b question. To get the change in entropy of the surroundings for the JT process, you first treat the surroundings as a separate system, and then devise an alternative reversible path between the same initial and final states it experienced in the irreversible process. In the case of the JT process, the initial and final states of the surroundings are identical. So it experienced no change in entropy in the JT process.

 

[WWCY]

In the case of the JT process, the initial and final states of the surroundings are identical. So it experienced no change in entropy in the JT process.

In the JT scenario, I managed to show explicitly that the surroundings did not change in state.

How do I show that in the case of the reversible isothermal expansion, the entropy of the surroundings change. The authors state that it will be equal to $-R\ln 2$, is it possible to show this in the way that I showed $dS_{surr} = 0$ for the JT scenario?

Also, what I meant by

If the quasistatic expansion represents a different physical process,

was that the JT case involved a sudden release of the tap and expansion of the gas, under thermally isolation from surroundings. In the quasistatic case, the act of integrating over the equation of state presumably means that the expansion was slow, perhaps like the slow expansion of gas in syringe at constant temperature. The changes in entropy within the system (container/syringe) are independent of path and both equal. However, the entropy change in their respective surroundings are not equal, how does one show this explicitly?

I do hope this is making sense.

 

[Chestermiller]

In the JT scenario, I managed to show explicitly that the surroundings did not change in state.

How do I show that in the case of the reversible isothermal expansion, the entropy of the surroundings change. The authors state that it will be equal to $-R\ln 2$, is it possible to show this in the way that I showed $dS_{surr} = 0$ for the JT scenario?

You do this by applying Step 1 of my recipe to the surroundings. In Step 1 of the reversible process, the surroundings supply heat to the system.

Also, what I meant by

was that the JT case involved a sudden release of the tap and expansion of the gas, under thermally isolation from surroundings. In the quasistatic case, the act of integrating over the equation of state presumably means that the expansion was slow, perhaps like the slow expansion of gas in syringe at constant temperature. The changes in entropy within the system (container/syringe) are independent of path and both equal. However, the entropy change in their respective surroundings are not equal, how does one show this explicitly?

I do hope this is making sense.

The irreversibility in your version of the JT expansion occurs within the stopcock where there is viscous dissipation of mechanical energy. It exactly takes the place of the effect of the rapid expansion when the barrier is rapidly removed.

 

[WWCY]

You do this by applying Step 1 of my recipe to the surroundings. In Step 1 of the reversible process, the surroundings supply heat to the system.

I keep getting the same (and wrong) result as the irreversible process. By conservation of energy, $dU_{surr} = 0$ since $dU_{sys}$ doesn't change in an isothermic reaction. Then, since $dV_{surr} = 0}$, it again leads me to $TdS_{surr} = 0$. What did I do wrongly?

 

[Chestermiller]

I keep getting the same (and wrong) result as the irreversible process. By conservation of energy, $dU_{surr} = 0$ since $dU_{sys}$ doesn't change in an isothermic reaction. Then, since $dV_{surr} = 0}$, it again leads me to $TdS_{surr} = 0$. What did I do wrongly?

Nothing. This is correct.

 

[WWCY]

Nothing. This is correct.

Apologies, but I'm not sure I follow. Isn't $\Delta S_{surr} = -R\ln2$ for the quasi-static process? I don't seem to be able to achieve this result.

Thank you for your patience.

 

[Chestermiller]

Apologies, but I'm not sure I follow. Isn't $\Delta S_{surr} = -R\ln2$ for the quasi-static process? I don't seem to be able to achieve this result.

Thank you for your patience.

What you are missing is that, for the reversible paths, the reversible path for the surroundings does not have to match the reversible path for the system. Each is subjected to a different reversible path to get the change of entropy of each (using new "surroundings" for each).

 

[Chestermiller]

Apologies, but I'm not sure I follow. Isn't $\Delta S_{surr} = -R\ln2$ for the quasi-static process? I don't seem to be able to achieve this result.

Thank you for your patience.

For the reversible isothermal process, the work done by the system on the surroundings is $RT\ln{\frac{V_2}{V_1}}=-RT\ln{\frac{P_1}{P_2}}$. And from the first law, since the expansion is isothermal, $$Q_{syst}=-RT\ln{\frac{P_1}{P_2}}=-Q_{surr}$$

 

[WWCY]

For the reversible isothermal process, the work done by the system on the surroundings is $RT\ln{\frac{V_2}{V_1}}=-RT\ln{\frac{P_1}{P_2}}$. And from the first law, since the expansion is isothermal, $$Q_{syst}=-RT\ln{\frac{P_1}{P_2}}=-Q_{surr}$$

I'm sorry but I am rather lost. In my calculation for the irreversible process, I defined the system to be the entire container, which includes the bit with gas, and the bit without gas. So my "surroundings" are everything outside the container.

However in your calculation for the reversible process, you seemed to have defined the system to only be the bit in the container with gas, and "surroundings" to be everything else, including the evacuated part of the container. Why is this so?

 

[Chestermiller]

I'm sorry but I am rather lost. In my calculation for the irreversible process, I defined the system to be the entire container, which includes the bit with gas, and the bit without gas. So my "surroundings" are everything outside the container.

However in your calculation for the reversible process, you seemed to have defined the system to only be the bit in the container with gas, and "surroundings" to be everything else, including the evacuated part of the container. Why is this so?

In the irreversible process, I agree that the system should be the total contents of the container, including both compartments (i.e., the gas).

For the reversible process applied to the same material (i.e., the gas), I take the gas out of the container and put it into a cylinder with a piston. I then hold the cylinder in contact with a constant-temperature reservoir at the same temperature as the gas, and allow the gas to expand quasi statically against a resistance force applied by the piston. In this alternative reversible process, the reservoir (and the force applied by the piston) constitute the alternative surroundings.

Did you read my tutorial? If so, please carefully reread Step 3 of the procedure.

 

[WWCY]

In the irreversible process, I agree that the system should be the total contents of the container, including both compartments (i.e., the gas).

Alternatively, would it be alright to think of the "system" as the part of the container with the gas, while the surroundings are "everything else"? And if so, could I conclude that the during the free-expansion, the gas does no work on the surroundings as the empty part of the container has $p = 0$?

Did you read my tutorial? If so, please carefully reread Step 3 of the procedure.

Yes I have, and it was very helpful. I just needed a concrete example, which I suppose I have now. Thank you!

 

[Chestermiller]

Alternatively, would it be alright to think of the "system" as the part of the container with the gas, while the surroundings are "everything else"? And if so, could I conclude that the during the free-expansion, the gas does no work on the surroundings as the empty part of the container has $p = 0$?

If you include only the part of the container with the gas (i.e., the left container), then it becomes an open system, since moles leave that part of the system. It is better to consider either the gas (or the entire container) as the system. In either case, no work is done by the system, and the system is closed.[/QUOTE]