alpha358
- 9
- 0
I don‘t understand one step in derivation of ideal gas chemical potential.
Generally Gibbs free energy is:
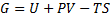 (1)
(1)
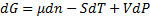 (2)We observe that:
(2)We observe that:
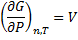 (3)From equation (3) we make differential equation and integrate it:
(3)From equation (3) we make differential equation and integrate it:
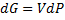 (4)
(4)
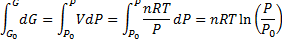 (5)
(5)
We get Gibbs free energy dependence on pressure:
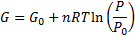 (6)
(6)
Equation (6) is true strictly when:
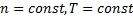 , because of equation. (3).
, because of equation. (3).
Later we derive chemical potential for ideal gas:
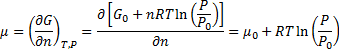 (7)
(7)
Here we assumed that
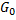 is a function of n. (because it is an extensive property), therefore:
is a function of n. (because it is an extensive property), therefore:
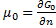
In the end we get pressure dependency of chemical potential for ideal gas:
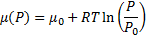 (8)
(8)
Note that in equation (7) we differentiate equation (6) by n and eq. 6 is derived only for condition when n = const and T = const.
In other words, we differentiate it with respect to variable which should stay constant.
Are we allowed to do this ?
Generally Gibbs free energy is:
We get Gibbs free energy dependence on pressure:
Later we derive chemical potential for ideal gas:
In the end we get pressure dependency of chemical potential for ideal gas:
Note that in equation (7) we differentiate equation (6) by n and eq. 6 is derived only for condition when n = const and T = const.
In other words, we differentiate it with respect to variable which should stay constant.
Are we allowed to do this ?
Last edited: