Thermodynamics: ideal gas chemical potential

[Lordgraver]

Can someone explain me why we could put p_i, μ_i and μ_i^ο in
this equation:

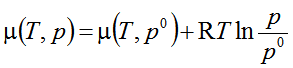
and we get this:

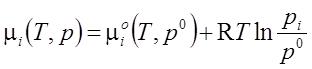
(this is The chemical potential of a component in a perfect mixture of ideal gases wher p_i is
partial pressure)

 

[DrDu]

Basically, this is the definition of a perfect mixture, i.e. the partial pressure of a component in the mixture is equal to the pressure of the pure component being in equilibrium contact via a semipermeable membrane being permeable only for this component.

 

[Lordgraver]

ok... Can you enlighten me as to prove this equation? How to start it?

 

[DrDu]

If the gas in the mixture and the free gas on the other side of the semipermeable membrane are in equilibrium when the partial respective total pressures are equal then also the chemical potentials must be equal and have the same dependence on the respective pressures.

 

[Chestermiller]

See Chapter 10 of Introduction to Chemical Engineering Thermodynamics by Smith and Van Ness.

Chet