jisbon
- 475
- 30
- Homework Statement
- Consider a ship mass of 2000000kg with propeller blades of radius 7m and it can push backwards to a speed of 2m/s. Given that density of water is 1000kg/m^3 , find acc of ship.
- Relevant Equations
- F=ma
upthrust = pgv
Hello.
Not sure how to even begin with this question honestly. Didn't learn anything about thrust regarding this topic so it got me dumbfounded.
Here's how I try to interpret it:
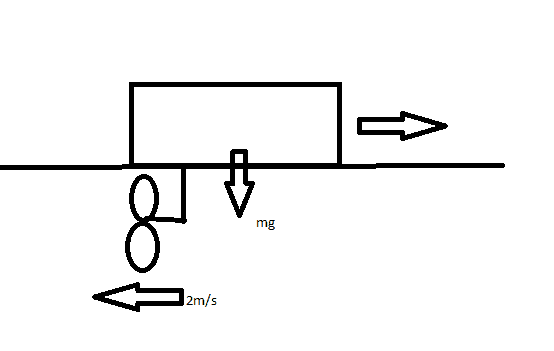
I'm assuming that the thrust created by propellers = net force of the ship, where I can use F=ma to find acceleration. The problem is I don't really know and understand how to calculate thrust using the density of water and velocity/radius of propeller. Any help will be grateful here. Thanks
Not sure how to even begin with this question honestly. Didn't learn anything about thrust regarding this topic so it got me dumbfounded.
Here's how I try to interpret it:
I'm assuming that the thrust created by propellers = net force of the ship, where I can use F=ma to find acceleration. The problem is I don't really know and understand how to calculate thrust using the density of water and velocity/radius of propeller. Any help will be grateful here. Thanks
Last edited by a moderator: