Time constant in an RC circuit

[VenaCava]

Homework Statement

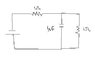
Find the time constant

Homework Equations

T=RC

The Attempt at a Solution

I understand the calculation fine. But I was wondering if the resistors are considered to be in parallel with each other even though the second resistor appears to be in parallel only with the capacitor?

so T=RC=(0.5 ohm)(1x 10^-6 F) = ... etc

Thanks

 

[hikaru1221]

Only in the case of RC circuit (the circuit comprises of R, C and the source all connected in series) is the time constant equal to RC. The circuit in the picture is not RC circuit and thus there is a need for analyzing this circuit.
Try to solve for the current i through capacitor C or the charge q on C. The solution should contain a time-dependent exponential term which is in this format: exp(-t/T). Here T is the time constant needed.
Hint: You will see that T = RC/2, not RC.

 

[VenaCava]

If I were to say that R= equivalent resistance of the entire circuit, would T=RC be correct?

Where R1= 1 ohm R2 = 1 ohm and R = 1/(1/1 + 1/1) = 0.5 ohm
so T=RC? or would this still be incorrect?

 

[Quinzio]

You apply Thevenin to solve the generator and two resistances.
The equivalent circuit is a V/2 generator in series with an R/2 resistance.
So the time constant becomes RC/2.

The capacitor voltage is

$$v_c(t) = \frac{V}{2}\left(1-e^{\frac{-2t}{RC}} \right)$$

 

[hikaru1221]

If I were to say that R= equivalent resistance of the entire circuit, would T=RC be correct?

Where R1= 1 ohm R2 = 1 ohm and R = 1/(1/1 + 1/1) = 0.5 ohm
so T=RC? or would this still be incorrect?

That's just for this particular circuit. If you convert the part containing the source and the 2 resistors into its Thevenin equivalent (only C is left), the Thevenin resistor is the equivalent resistor of (R1 // R2).

 

[VenaCava]

I am not familiar with the Thevenin equivalent...

When a capacitor is fully charged, does it act as a plain wire? I can't recall, sorry its been ages since I studied capacitor/circuit basics.

Would it be correct to say that while the battery is still connected (ie before the capacitor is discharged) that

Vbat= IR1 + Q/C

Is this equation at all useful to me?

 

[hikaru1221]

When a capacitor is fully charged, does it act as a plain wire?

An ideal capacitor won't. Please have a look on Wikipedia

Would it be correct to say that while the battery is still connected (ie before the capacitor is discharged) that

Vbat= IR1 + Q/C

Is this equation at all useful to me?

Yes and yes. The equation shows what happens and also what must happen in the circuit.

 

[VenaCava]

So from there, how can I use that equation to find the time constant? I don't have the voltage value or current, so I'm assuming these will have to cancel out somewhere and are therefore independent of the time constant. I'm think my the time constant will only be based on the capacitance and the ratio/values of the resistors but I'm not sure how I get to this stage.

 

[VenaCava]

Okay, let me rephrase this. You guys say that the time constant is T=RC/2. However, if this were for two different values of R (ie. R1 and R2, which don't have the same value) how would this change the time constant and what would it equal (what is T, in terms of C, R1, and R2)?
Thanks!

 

[hikaru1221]

So from there, how can I use that equation to find the time constant? I don't have the voltage value or current, so I'm assuming these will have to cancel out somewhere and are therefore independent of the time constant. I'm think my the time constant will only be based on the capacitance and the ratio/values of the resistors but I'm not sure how I get to this stage.

Actually you have an equation for current: i = current through R parallel to C + current through C.
_ The current through C is dq/dt.
_ The current through R parallel to C = voltage across it / R, and that voltage is the same as the voltage across the capacitor.
You will then have to solve a differential equation.

Okay, let me rephrase this. You guys say that the time constant is T=RC/2. However, if this were for two different values of R (ie. R1 and R2, which don't have the same value) how would this change the time constant and what would it equal (what is T, in terms of C, R1, and R2)?
Thanks!

In this particular problem, T = R_eqC, where R_eq is the equivalent resistance of (R1 // R2). Solve the differential equation and you will see this

 

[VenaCava]

My question I posted is actually based on a laboratory experiment. While the value of the resistors were the same in the lab, they had different error values associated with them, so ideally I'm trying to find a value for T that is a function of R1 and R2 (so I can calculate the error value that goes along with my calculated time constant). Is it possible to express T in terms of these two values?

By the way, thank you so much for your help so far! I really appreciate it.

 

[Quinzio]

Okay, let me rephrase this. You guys say that the time constant is T=RC/2. However, if this were for two different values of R (ie. R1 and R2, which don't have the same value) how would this change the time constant and what would it equal (what is T, in terms of C, R1, and R2)?
Thanks!

If you're studying electronic in depth you have to become familiar with Thevenin. It is really udeful.$$v_c(t) = \frac{VR_1}{R_1+R_2}\left(1-e^{\frac{-t}{\tau}} \right)$$

$$\tau = C\frac{R_1R_2}{R_1+R_2}$$

 

[Quinzio]

I am not familiar with the Thevenin equivalent...

When a capacitor is fully charged, does it act as a plain wire?

Nope. As an open circuit.

 

[VenaCava]

If you're studying electronic in depth you have to become familiar with Thevenin. It is really udeful.


$$v_c(t) = \frac{VR_1}{R_1+R_2}\left(1-e^{\frac{-t}{\tau}} \right)$$

$$\tau = C\frac{R_1R_2}{R_1+R_2}$$

Thank you! This is perfect. I tried to derive it myself but was not successful. Would this be possible for me to do without Thevenin (as I have not learned it yet)?

 

[hikaru1221]

Yes, by solving the differential equation
The 2 equations needed are:

_Voltage equation: $$V_{bat}=iR_2 + q/C$$ (*)

_ Current equation: $$i = \frac{dq}{dt} + i_{R1} = \frac{dq}{dt} + \frac{V_{R1}}{R_1}$$

But $$V_{R1} = q/C$$, so: $$i = \frac{dq}{dt} + \frac{q}{CR_1}$$ (**)

_ Substituting (**) into (*):
$$V_{bat} = (\frac{dq}{dt} + \frac{q}{CR_1})R_2 + \frac{q}{C}=R_2\frac{dq}{dt} + \frac{R_1+R_2}{CR_1}q$$

The next step is to solve this differential equation The general solution will definitely contain the term $$e^{-t/T}$$ where T is the time constant as Quinzio pointed out. But the exact solution depends on the initial conditions, which are not mentioned here, so I'll leave it aside. We only need to show that there is the exponential term in the solution

 

[VenaCava]

So if for this particular circuit, I am discharging the capacitor, would this be correct for solving the differential eq?
(PS sorry I don't know how to do the pretty equations)

Vbat = R2 dq/dt + (R2 + R1)q/CR1 (since the circuit is being disconnected from the voltage source at t=0 vbat=0 ?)

dq/dt = -(R2 + R1)q/CR1R2

Q= Q(t=0) e^{(-t/ CR1R2/(R2 + R1))}

therefore T= CR1R2/(R2 + R1)

 

[hikaru1221]

You are right at deducing that V(battery)=0 when there is no battery (discharge) The same trick is used in many circuit analysis methods.

 

[VenaCava]

Thank you so much!