Time it takes for a capacitor to lose half of its energy

[sliperyfrog]

Homework Statement

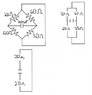
In the circuit below (drew it the best I can) the switch is opened, how much time elapses before the capacitor loses half of its initial stored energy.

Homework Equations

[/B]
q(t) = Qe^-t/RC

U = q²/2C

The Attempt at a Solution

[/B]
So first thing I did was I set (1/2)Q²/2C = q²/2C then i replaced q² for Q²e^-2t/RC so I get (1/2)Q²/2C = Q²e^-2t/RC/2C I cancel out the like terms and I am left with 1/2 = e^-2t/RC I than get rid of the e so I get ln(1/2) =-2t/RC then i get -ln(2) = -2t/RC getting me t = RCln(2)/2 and now this is were i got confused I know C = 200E-6 F but i don't know what R is suppose to be, I think it is suppose to be 90Ω since the 30Ω and the 60Ω resistors connect together at where the capacitor is.

 

[cnh1995]

Draw a separate circuit diagram for discharging without the 90V battery. In which fashion are the resistors connected?

 

[sliperyfrog]

Okay so i redrew it and i found out it was parallel so I did (1/60 + 1/30)^-1 = 20Ω but now i am confused on whether the R in the equation is 20Ω or 40Ω since the current goes through the first 20Ω then the capacitor then another 20Ω.

 

[cnh1995]

Okay so i redrew it

That's not correct. Why have you drawn the external loop joining the two junctions? The discharging circuit will contain only the 4 resistors and the capacitor.

 

[sliperyfrog]

Why have you drawn the external loop joining the two junctions?

I was thinking that since that loop that connects the battery was in the original circuit that the junction that connect to the battery would still be there.

 

[cnh1995]

I was thinking that since that loop that connects the battery was in the original circuit that the junction that connect to the battery would still be there.

No. The switch is "opened" and the loop is disconnected from the circuit.

 

[sliperyfrog]

So then the circuit would look like this

And now I am back to the problem i was struggling with before is the two 90Ω resistors in parallel or is the capacitor in the the middle stopping it?

 

[cnh1995]

So then the circuit would look like this View attachment 110280 And now I am back to the problem i was struggling with before is the two 90Ω resistors in parallel or is the capacitor in the the middle stopping it?

They are in parallel. In fact, the capacitor too is in parallel with them. Review the theory of series and parallel components to avoid any further confusion.

 

[sliperyfrog]

So since they are in parallel that means the R in the problem is (1/90 + 1/90)^-1 = 45Ω so for the answer I would get t = (45)(200E-6)ln(2)/2 = .0031s

 

[cnh1995]

So since they are in parallel that means the R in the problem is (1/90 + 1/90)^-1 = 45Ω so for the answer I would get t = (45)(200E-6)ln(2)/2 = .0031s

Looks good.