VSayantan
- 57
- 4
Homework Statement
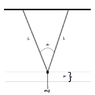
[/B]A heavy mass ##m## is suspended from two identical steel wires of length ##l##, radius ##r## and Young's modulus ##Y##, as shown in the figure above. When the mass is pulled down by a distance ##x## ##(x<<l)## and released, it undergoes elastic oscillations in the vertical direction.
What is the time period?
Homework Equations
Equation of motion of a harmonic oscillator
$$m\frac {d^2 x} {dt^2} = -kx$$
where, ##k## is the spring constant.
Young's modulus of a wire of length ##l##, radius ##r## is
$$Y = \frac {FA} {l \cdot \Delta l}$$
Time period
$$T = \frac {2\pi} {\omega}$$
The Attempt at a Solution
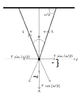
The vertical components of tension cancel out, while the horizontal components add.
At equilibrium
$$k \cdot l \cdot cos {\frac a 2} = mg$$
With the given small displacement ##x<<l##
$$F=k[l \cdot cos {\frac a 2} + x] -mg$$
$$\Rightarrow m \frac {d^2 x} {dt^2} = -kx$$
$$\Rightarrow \frac {d^2 x} {dt^2} = -\omega^2 x$$
Where ##\omega = \frac k m = \frac {mg} {m \cdot l \cdot cos {\frac a 2}} =\sqrt {\frac {g} {l \cdot cos {\frac a 2}}}##
So time period
$$T = \frac {2\pi} {\sqrt {\frac {g} {l \cdot cos {\frac a 2}}}} = 2\pi \sqrt {\frac {l \cdot cos {\frac a 2}} {g}}$$
But, I cannot use the expression for the Young's modulus. What am I missing?