serverxeon
- 100
- 0
I have a hemisphere dome, which volume = \frac{2}{3}∏r3
Inside the dome, pressure is 1atm (assume 1.05 kPa)
Outside the dome, pressure is 0.01atm (10.5 Pa)
I then puncture a 0.2 cm2 (2 x 10-5 m2) hole on the flat side of the dome.
Question: Find time taken for pressure to equalise.
--------------
I have searched up the internet, and seems that I have to use bernoulli. But I have a few problems.
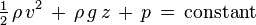
1) I have no idea what to substitute for the variables.
2) Are the density of air inside and outside the dome different?
3) How should I use calculus (or differential equations, or anything else) to find the time taken, given the process is non-linear in relation.
Thanks
Inside the dome, pressure is 1atm (assume 1.05 kPa)
Outside the dome, pressure is 0.01atm (10.5 Pa)
I then puncture a 0.2 cm2 (2 x 10-5 m2) hole on the flat side of the dome.
Question: Find time taken for pressure to equalise.
--------------
I have searched up the internet, and seems that I have to use bernoulli. But I have a few problems.
1) I have no idea what to substitute for the variables.
2) Are the density of air inside and outside the dome different?
3) How should I use calculus (or differential equations, or anything else) to find the time taken, given the process is non-linear in relation.
Thanks
Last edited: