gnits
- 137
- 46
- Homework Statement
- To find the reaction in a system at a ring
- Relevant Equations
- moments
Could I ask for a hint as to where to go next with this question please?
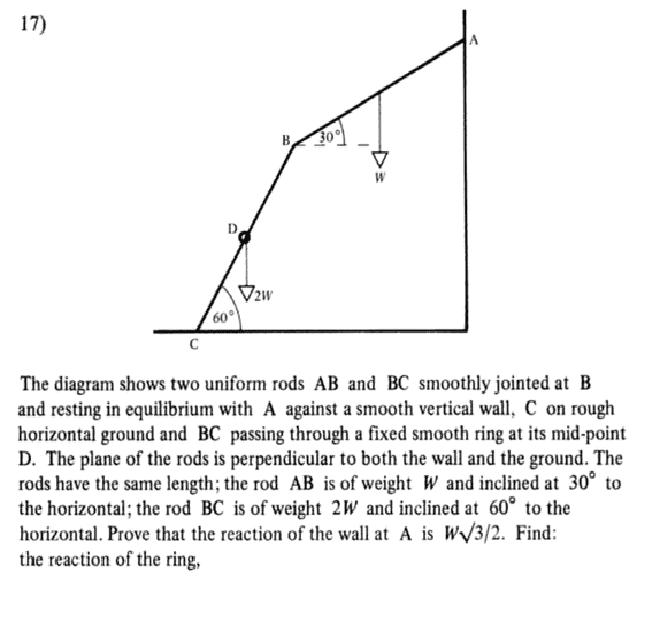
I've done this first part, to find the reaction on the wall. Here's my diagram:
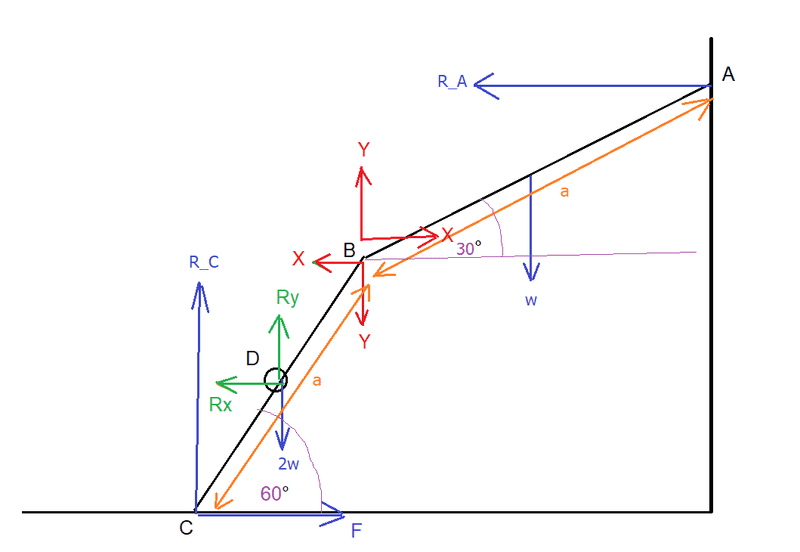
I've labelled the internal forces at B in red.
In green I've shown the reaction at the ring.
So I need to find sqrt(Rx^2 + Ry^2) = R.
So I need to find Rx and Ry in order to calculate R.
For the whole system:
Vertically: R_C + Ry = 3w
Horizontally: R_A + Rx = F
For BA only:
Vertically Y = w
Horizontally: R_A = X
Moments about B gives: R_A * a sin(30) = w * (a/2) * cos(30) which yields R_A = sqrt(3)*W/2 as required.
Now that we know R_A, for whole system:
Taking moments about C leads to: sqrt(3)*Rx + Ry = w
Not sure how to proceed.
If I take moments about C for BC only, this leads to the same equation sqrt(3)*Rx + Ry = w
If I take moments about D for BC only this yields: R_C - sqrt(3)*F = w/2
All my answers above are consistent with the book answer, but I can't see how to proceed.
Book answers is: R = sqrt(Rx^2 + Ry^2) = w/2
So, I am trying to find Rx and Ry in order to calculate R.
Thanks for any pointers.
I've done this first part, to find the reaction on the wall. Here's my diagram:
I've labelled the internal forces at B in red.
In green I've shown the reaction at the ring.
So I need to find sqrt(Rx^2 + Ry^2) = R.
So I need to find Rx and Ry in order to calculate R.
For the whole system:
Vertically: R_C + Ry = 3w
Horizontally: R_A + Rx = F
For BA only:
Vertically Y = w
Horizontally: R_A = X
Moments about B gives: R_A * a sin(30) = w * (a/2) * cos(30) which yields R_A = sqrt(3)*W/2 as required.
Now that we know R_A, for whole system:
Taking moments about C leads to: sqrt(3)*Rx + Ry = w
Not sure how to proceed.
If I take moments about C for BC only, this leads to the same equation sqrt(3)*Rx + Ry = w
If I take moments about D for BC only this yields: R_C - sqrt(3)*F = w/2
All my answers above are consistent with the book answer, but I can't see how to proceed.
Book answers is: R = sqrt(Rx^2 + Ry^2) = w/2
So, I am trying to find Rx and Ry in order to calculate R.
Thanks for any pointers.
Last edited: