BrownBoi7
- 24
- 0
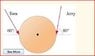
Tom and Jerry both push on the 3 m diameter merry-go-round shown in the figure attached.
(a) If Tom pushes with a force of 40 N and Jerry pushes with a force of 35.2 N, what is the net torque on the merry-go-round?
(b) What is the net torque if Jerry reverses the direction by 180 degrees without changing the magnitude of his force?
My attempt:
FT = Force exerted by Tom = 40 N
FJ = Force exerted by Jerry = 35.2 N
T = Torque = RF sinΘ
TT = 1.5 m * 40 N * sin 60 = 1.5 m * 40 N * -0.304 = -18.28 Nm
TJ = 1.5 m * 35.2 N * sin 80 = 1.5 m * 35.2 N * -0.993= --52.43 Nm
(a) Net T= -18.28 Nm + (- 52.43 Nm) = -70.71 Nm
(b) When Jerry reverses,
Net T = -18.28 Nm - (-52.43 Nm) = 34.15 Nm
My answers didn't match my professor's answers. I believe I went about it the right way. Could somebody please point out where I messed up?
Thanks!
(a) If Tom pushes with a force of 40 N and Jerry pushes with a force of 35.2 N, what is the net torque on the merry-go-round?
(b) What is the net torque if Jerry reverses the direction by 180 degrees without changing the magnitude of his force?
My attempt:
FT = Force exerted by Tom = 40 N
FJ = Force exerted by Jerry = 35.2 N
T = Torque = RF sinΘ
TT = 1.5 m * 40 N * sin 60 = 1.5 m * 40 N * -0.304 = -18.28 Nm
TJ = 1.5 m * 35.2 N * sin 80 = 1.5 m * 35.2 N * -0.993= --52.43 Nm
(a) Net T= -18.28 Nm + (- 52.43 Nm) = -70.71 Nm
(b) When Jerry reverses,
Net T = -18.28 Nm - (-52.43 Nm) = 34.15 Nm
My answers didn't match my professor's answers. I believe I went about it the right way. Could somebody please point out where I messed up?
Thanks!