Box Toppling: Causes and Effects

[adjacent]

I don't know if "toppling" is even a word.

This is not a homework,just a question.
https://www.physicsforums.com/attachment.php?attachmentid=68762&stc=1&d=1397811697
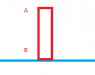
If I apply a force at A,the box will topple and fall.(Probably because of friction)
If I apply a force at B,the box will move(Probably because the force overcame the friction)

What's causing it? Torque?
As the distance increase,the effect of force on friction decreases but why?

P.S I am a Grade 10 student.

 

[SteamKing]

'toppling' is the present participle of the verb 'to topple', just like 'running' is the present participle of the verb 'to run'.

What can you say about the location of A or B w.r.t. the center of gravity of the box?

 

[voko]

There is a problem with the attachment, I cannot see the picture. Generally, it is safe to say that "toppling" involves torque.

 

[adjacent]

Here is the image.

I don't think this problem involves Center of Gravity.When I push B,the box does not topple at all.

 

[voko]

If the force at B is great enough, the box will topple. Counter-clockwise.

 

[Radarithm]

Here is the image.

I don't think this problem involves Center of Gravity.When I push B,the box does not topple at all.

When you apply the torque at the bottom, there is friction to oppose it (I think).
When you apply it to the top (A), there is no friction to oppose it except air resistance.
Are the forces equal?

EDIT: the reason the friction decreases as the distance increases is because of kinetic friction being less effective than static friction.

 

[adjacent]

If the force at B is great enough, the box will topple. Counter-clockwise.

No.We are applying the same force on both A and B. But it only topples when we apply the force on A.
It only moves horizontally to right when we apply a force on B.
So there should be some relationship between the distance the force is applied and whether it should topple or not.

 

[adjacent]

When you apply it to the top (A), there is no friction to oppose it except air resistance.

I don't think so.There is still the friction at the bottom.If there is not friction,it would only move without rotating(It will rotate about the center of gravity.But here it is rotating about a point at the bottom)

Are the forces equal?

Yes.

 

[voko]

No.We are applying the same force on both A and B. But it only topples when we apply the force on A.

This really depends on the magnitude of the force. A force great enough, applied either at A or B, will have the box topple, in different directions.

The minimal forces required for that at A or B may be different, however. Radarithm explained one reason for that.

 

[adjacent]

EDIT: the reason the friction decreases as the distance increases is because of kinetic friction being less effective than static friction.

What do you mean by "less effective"?

 

[Radarithm]

What do you mean by "less effective"?

\mu_s N\ > \mu_k N

Where mu sub s is the coefficient of static friction, the other one is kinetic friction.

 

[Radarithm]

http://en.wikipedia.org/wiki/Friction#Static_friction
Under it is the one for kinetic friction.

 

[amind]

For what I know it is torque, initially the box is at rest , when the box topples it is because you disturbed its equilibrium and there is a net torque due to its weight.

In both cases,
You apply a force F at the point A or B,
Consider its bottom right point as the axis of rotation.
It is clearly visible that the moment arm of A is greater than B.
Note : The box toppled because the angular inertia of this box is less and it was easier to overcome the torque, otherwise its angular inertia will be more and the linear equilibrium would have been easier to disturb.
Note 2 : As someone stated earlier if you apply a big enough force at B , the box would topple the other way , this is also because it was easier to turn it with the center of box as axis , also note that it is totally dependent on the static friction,
Since while toppling the axis of rotation is stationary w.r.t the floor.

 

[adjacent]

uhh. What's angular inertia and linear equilibrium?

 

[SteamKing]

uhh. What's angular inertia and linear equilibrium?

This is where you start studying physics to find the answers.

 

[adjacent]

This is where you start studying physics to find the answers.

As I said before,I'm just a Gr.10 student.
OK,I'll try to solve this after A-levels and see if I can really solve it.

 

[Radarithm]

Just like how a Torque is the angular counterpart of a Force, Angular inertia is the angular counterpart of linear inertia, which is an object's "resistance" to forces.

 

[amind]

uhh. What's angular inertia and linear equilibrium?

Just like in linear (straight , no rotation) motion , we have mass/inertia defined as the force required to produce a unit acceleration ,
By Newton's law,
m = F/a,
So the analogous angular variables,
Angular Inertia (I) = Torque (\tau) / Angular acceleration(\alpha)

When I meant linear equilibrium , I meant the one involving linear variables , while the other type of equilibrium is angular.

Hope that clear things up.