cupcake_rainbow
- 2
- 0
- Homework Statement
- Two weights P and Q are suspended from a fixed point 0 by strings OA, OB and are kept apart by a light rod AB. If the strings OA and OB make angles alpha and beta with the rod AB, show that the angle theta which the rod makes with the vertical is given by tan theta = (P+Q)/(Pcot alpha -Qcot beta)
- Relevant Equations
- torque balancing
So I tried using force balancing.
I have attached files of my solution in my notebook
Torque balancing about O which gives me equation 1
And I used property of triangle, for equation 2
But i can't seem to get the right answer
Also, I was wondering if it could be done by concept of virtual work.

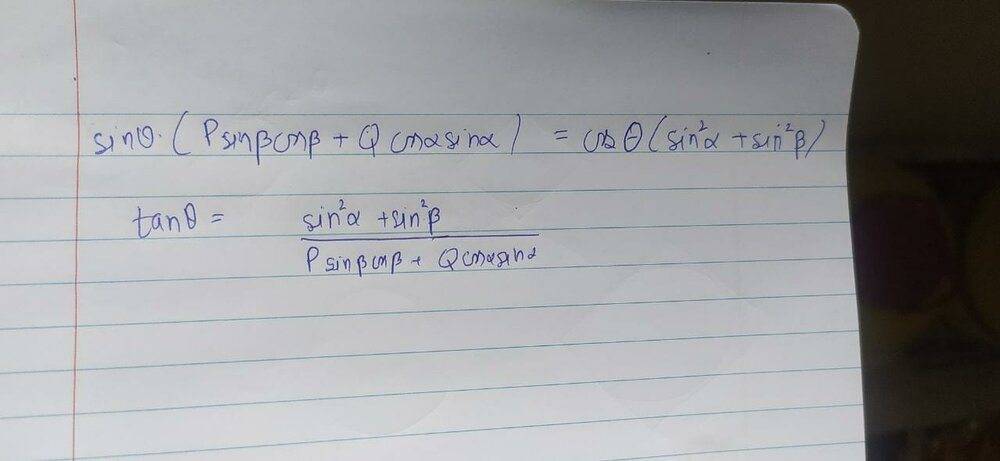
I have attached files of my solution in my notebook
Torque balancing about O which gives me equation 1
And I used property of triangle, for equation 2
But i can't seem to get the right answer
Also, I was wondering if it could be done by concept of virtual work.