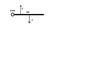Can torque be fully understood through classical mechanics alone?

[aaaa202]

I have now finished my lectures on classical mechanics, but I'm a bit ashamed to say that I still don't understand the concept of torque fully.

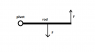
Let's imagine this. We have a rod being acted on by the equal and opposite forces, but in different distances from the centre of rotation (attached picture). This then means that the rod will start rotating anticlockwise. To understand why the upwards force is more efficient in rotating the object we can apply an energy observation: Since the object is a rigid, rotating object, the power from the force farthest away from the rotation centre will be greater, and thus the rod will rotate anticlockwise.

Now, that observation helps me understand torque. The problem is that it does not really apply to all cases. Consider this: When the object has not started to rotate yet, there will be no power from neither of the two forces. Yet everyone knows that the object will INDEED start to rotate.

Does this mean that torque can't be understood in terms of concepts like momentum and energy? - i.e. concepts that I recognize from linear dynamics.

I ask this because the derivations in my book somehow always assume that the object to which we apply a torque is rotating already - thus they indirectly use the energy observation made earlier. But that cannot explain the case, where the object has not yet started rotating. Would this be an empirical observation? I mean, that we define angular momentum from torque, which applies to an object already rotating, but then we find out that the concept works on an even deeper level - i.e. in the case where the angular velocity is zero..

That was a lot of questions, but I have never got a good answer from anyone to this question - that is my teachers etc. etc.
If in some deeper way this actually can be explained through Lagrangian- and Hamiltonian mechanics, you are welcome to say that - I just don't like the feeling of not understanding a concept fully...

Cheers :)

 

[Studiot]

Wow, perhaps your difficulty is that you are trying too hard.

Now, that observation helps me understand torque. The problem is that it does not really apply to all cases. Consider this: When the object has not started to rotate yet, ...

...I ask this because the derivations in my book somehow always assume that the object to which we apply a torque is rotating already

The textbook 'assumes' that the object is rotating because it cannot be doing anything else

In particular it is not in equilibrium.

There is no such thing as 'just started to rotate' with, for instance, the lever system you have shown. If it is not rotating it is being held against rotation by another force that you have not shown.

Does this help?

 

[aaaa202]

Certainly you can observe a situation like mine, but perhaps I didn't make it clear enough what I meant.

Suppose you have something supporting the rod and then removed it. It would obviously initiate a rotation, because it is NOT in equilibrium - i.e. the net torque on it is not zero. The torque can explain why it will rotate as soon as the object has started its rotation - but the initian phase can as I see it not be understood in terms of energy concepts.

But perhaps a torque is just a knew concept not really related to linear dynamics. In linear dynamics after all you can't really explain why something is accelerating due to a force just using energy concepts.

I must admit, that I look forward to see if lagrangian and hamiltonian dynamics give a whole new way of understanding clasiccal mechanics.

 

[Studiot]

Langrangian and Hamiltonian views of mechanics don't involve comparing two systems with different characteristics any more than the Newton view does.
Another way to put this would be to say that we don't change the system part way through the path, as removing a restraint or force would do.

 

[aaaa202]

Then I'm just saying that there must be some empirical, in the way that torque behaves in nature, which can't be shown with the equations I have seen.

Either that or you can't use energy concepts to understand torque completely.

I'm thinking the last one, is probably the right one.

 

[Studiot]

I am sorry I am not explaining myself very well.

Firstly you have two different, independent mechanical systems.

1) The system at rest with restraint to balance forces and moments. Since it is at rest there are no energy considerations, although as an arrangement of forces and reactions energy theorems such as that of Maxwell, Betti et al may be deployed.

2) A second, different and independant, system after the restraint has been removed.

Let us take a linear motion example first.

Consider a projectile mounted in a catapault, or an arrow held in a taught bow by an archer.
We can define the forces in the bow or catapault string and therefore the necessary restraint.
The model is adequate to fully describe the situation

This is situation (1) above.

Now remove the restraint. the catapault or bow fires and the projectile accelerates forwards to its terminal velocity.
The projectile does not instantly achieve its terminal velocity.
It goes through a startup process as you envisage.
To model this startup process you need details of the elastic properties of the catapault or bow to find the elastic strain energy and model its transfer to the projectile.
You also need details of the inertial resistance of the projectile.

This is situation (2) above.

Now consider your rod in its pivot.

In situation (1) the rod is restrained and no energy is involved.

The model is adequate to fully describe the situation.

In situation (2) the restraint is suddenly removed and the rod commences rotation.
It does not reach its terminal angular velocity instantly.
To model this startup process you need details of the rotational inertia of the rod and the stiffness or otherwise of the driving forces F, just as above.

In short you model is missing some things.

Does this help?

 

[aaaa202]

hmm no, I think we are discussing two different things. Mainly I think that is because the situation i set up doesn't really deliver the point I want.

So I think what's wrong with my understand, is perhaps that I don't understand why the center of mass will make a downwards motion.
Consider the attached picture, which is a modified model of the rod, where now, the downwards torque is bigger. You could see this as the weight of the rod, and then the other force would be a person pushing upwards on the rod.

Due to the sum of torques being different from zero it will start to rotate downwards.

But at the same time, the rod would obey the linear equation of forces for its center of mass. That is that zero net force means zero acceleration. But clearly if it rotates the center of mass will fall downwards. So what explains this? Is it wrong to see the geometric center of the rod as the center of mass in this case?

Similarly I don't understand the opposite case. That is, if you have an equilibrium because the resultant torque is zero. This could be achieved by having a force in one distance from the rotational centre, and then another with half the magnitude but in twice the distance. Yet certainly the center of mass would not be in equilibrium, and would have to fall downwards or upwards depending on the convention.

 

[Doc Al]

But at the same time, the rod would obey the linear equation of forces for its center of mass. That is that zero net force means zero acceleration. But clearly if it rotates the center of mass will fall downwards. So what explains this? Is it wrong to see the geometric center of the rod as the center of mass in this case?

The net force is not zero. Don't neglect the force from the pivot.

 

[aaaa202]

So you are suggesting that the pivot pushes down on the rod? How on Earth can it do that? Usually a force from a pivot comes through a reaction, but there's not really anything pushing up against the pivot, which could explain that it pushed down.

 

[Doc Al]

So you are suggesting that the pivot pushes down on the rod? How on Earth can it do that? Usually a force from a pivot comes through a reaction, but there's not really anything pushing up against the pivot, which could explain that it pushed down.

Yes, the pivot pushes down on the rod. (You have an upward force on the rod, which leads to that reaction force at the pivot.)

If you don't think the pivot is pushing down, then remove it and see what happens.

 

[Studiot]

Once again your diagram is incomplete.

Have you tried the analysis with Doc Al's comment incorporated?

Attached is an equilibrium analysis.
You cannot apply forces as you have shown without restraint or motion because the system is not in equilibrium.
For equilibrium without other restraint the applied upward force (I have called it F) has to be greater than the applied downward force (I have called it W) by the value of the vertical hinge force.
In this case you have the moment equilibrium maintained as the product of the larger force and the smaller lever distance equal to the product of the larger lever distance and the smaller force.

It really is easier to see as a diagram than in words.

This is fundamental to the setup as a machine with mechanical advantage or if you like the fact that to maintain equilibrium you have to push up with a greater force than the weight of the plank if you push up at a point between the plank centre and the pivot.

 

[aaaa202]

hmm. Upwards force on the rod? :(
Surely the sum of forces on the rod is zero. What is not zero is the torques. So would you then understand the non-zero net torque as something that makes the rod push up against pivot making the whole system rotate downwards?

 

[Doc Al]

hmm. Upwards force on the rod? :(

Yep. Look at your diagram.

Surely the sum of forces on the rod is zero.

Only if you ignore the force from the pivot.

What is not zero is the torques. So would you then understand the non-zero net torque as something that makes the rod push up against pivot making the whole system rotate downwards?

You can think of it that way. The only way that the center of mass can accelerate downward is if there is net downward force on the rod.

 

[Studiot]

What is not zero is the torques

The equilibrium torques (I prefer to use the term moments) sum to zero as I have shown.

 

[aaaa202]

Yes okay I see now, that I should have incorporated the force from the pivot point. Yet I don't really understand what causes the pivot to push down on the rod.

That force must come from rod pushing up against the pivot. But again that must mean that the rod is moving upwards.. Clearly it's not. Though the sum of torques is nonzero. So that'd be the only thing explaining that the rod pushes up against the pivot.

But then we're finally back to the original discussion of how I don't understand torque when energy observations can't be applied.

 

[aaaa202]

I think I'm going in circles. I'm afraid my whole approach to mechanics is probably not right.
I see it as this:

First we take the rod without the force from the pivot and try to understand what makes the force from the pivot appear. In that case we will have that the net torques makes the object push against the upper part of the pivot making it push down such that center of mass translates downwards.

But maybe it's wrong to do it like that. You have to understand the forces as something that appear instantly.

But I'm still left with the fact that torque can't be understood through energy in this case.

 

[Studiot]

I think I'm going in circles. I'm afraid my whole approach to mechanics is probably not right.

Yes, so try to follow the chain of reasoning through with us.

First take my amended version of your diagram.

Consider a plank, hinged at one end (P) with weight W acting downwards at L₂, halfway along the plank.

Apply a variable upward force F at some point between W and the hinge.

Let the hinge forces be Y horizontal and X vertical

Now consider what happens as we increase F from zero.

1) F=0

2) 0<F<W

3) F=W

4 F>W

5 F>>W

 

[Studiot]

One thing puzzles me.

You started this thread mentioning Hamilton and Lagrange. These are not usually taught until quite a high level of mechanics.

So what level are you studying at?

There is something known as 'the equation of energy', which is a precursor to Hamilton's methods which you could employ.

However it is important to get the basics of mechanics right first.

If I posted a derivation of this equation from the principles of angular and linear momentum would that help. It uses simple calculus.

 

[rcgldr]

First we take the rod without the force from the pivot and try to understand what makes the force from the pivot appear. In that case we will have that the net torques makes the object push against the upper part of the pivot making it push down such that center of mass translates downwards.

Assume the rod is rigid. When the forces are applied to the rod, the effect of those forces travel through the rod as the speed of sound in the rod. For most physics problems, the speed of sound within the rod is treated as if it is infinite, so that the force from the pivot occurs simultaneously with the other forces on the rod.

power ... energy

There is no issue here. Assume the initial state of the rod is that it is not moving, so it's inital energy state is zero. The resulting torque force on the rod increases it's (angular) kinetic energy over time (assming the rod has mass and angular inertia). If there are no drag forces, then rate of angular velocity continues to increase as long as the forces are applied. If the forces are constant, then power increases with the angular velocity of the rod.

pivot force ... downwards

The pivot force is initially upwards and always in the tangental direction of the end of the rod. The rod will be accelerating counter-clockwise in the diagram you included in your first post.

 

[aaaa202]

If I posted a derivation of this equation from the principles of angular and linear momentum would that help. It uses simple calculus.

Yes that might be very helpful.

I'm currently at the first year of university. I think assignments in mechanics tend to be very easy, but the underlying concepts can still be quite hard.

I've tried to follow your way, but I'm afraid to say that I still doesn't really help me in understanding.

How I understand things now:
If you have the rod attached to the pivot with the forces applied you can see it like this:
Initially the rod will try to rotate around its center of mass, since there is a net torque around this point. The rod will however push against the upper side of the pivot, making the system rotate downwards as you would expect.

 

[Studiot]

How I understand things now:
If you have the rod attached to the pivot with the forces applied you can see it like this:
Initially the rod will try to rotate around its center of mass, since there is a net torque around this point. The rod will however push against the upper side of the pivot, making the system rotate downwards as you would expect.

Yup that takes care of case (1) where F = 0.

It is important to realize that the hinge forces, X and Y will be what they need to be to make things work. Either may be zero.
Also we test whether the system is in equilibrium or motion by testing for zero resultants vertically, horizontally and zero net moment.

If all these three conditions are met the system is in equilibrium.
If not it is in motion with the resultants determining the motion.

It is important to get this sequence of logic this way round.


So case (1)

F=0
X=W at all times. Edit: X and W are in opposite directions as shown so really X = -W with signs
Y=0
Both X and Y pass through hinge and exert no moment about it.

But W exerts a moment about the hinge.

So the system is in motion, not equilibrium.

So the plank swings down until it is hanging vertically below P.
As the plank swings down the perpendicular distance from P to W decreases so the moment decreases until the distance is zero and the moment is zero and the plank is hanging.

This is a more complete analysis of case (1)

We should finish the others before moving on.

 

[aaaa202]

Yup that takes care of case (1) where F = 0.

hmm :)
I thought that took care of the case on my picture, where F equals the weight... I can see that it of course also would explain the case where F=0, but why not the original case with F=W?

Btw, I really appreciate all the help..

 

[Studiot]

Let's slowly build up through each case as each one is instructive. We will get there.

Case (2) is a little more complicated so here is another diagram and I will be more careful with the signs.

Did you note my edit - shows how easy it is to rush and miss something?

Let the plank make an angle θ with the vertical at any time.
And let F be normal to the plank at all times.

Case (2) 0<F<W

There are now horizontal forces acting, but since there is no horizontal translation:

Fcos(θ) = Y

Since there is no vertical translation of the system

Fsin(θ) = W ± X

But F < W and sin(θ) < 1 → Fsin(θ) < W so X must be opposite in sign to W ie upwards.

Since X and Y pass through P they exert no moment about P.

Summing Moments about P we have

L₁F - L₂Wsin(θ)

Which is not zero for all θ.
So the system in not in equilibrium it is in motion.
When the plank is horizontal θ = 90 so L₂Wsin(θ) > L₁F
So the plank commences to swing down

However as it swings down the moment developed by F remains constant but that developed by W diminishes as θ decreases.

Eventually a condition is reached, before the plank is vertical, where

L₁F = L₂Wsin(θ)

and rotation stops here - equilibrium is achieved.

In the next post we will consider the energy implications of cases (1) and (2).

 

[aaaa202]

hmm yes, I think I understand all this. Now I'm not sure if it builds up to a point, but I'm only interested in the instant that the rod starts rotating, only because of the moments around it. For me something can't possibly rotate just because of moments. But of course I'm wrong because if you push at the end of a wrench in outer space it will start to rotate - a puzzle to me, who can only understand torque through energy.
Now I know I'm repeating myself, but I can't really see if this is the end will make me understand, why torque is more than just energy considerations..

 

[Studiot]

I'm currently at the first year of university. I think assignments in mechanics tend to be very easy, but the underlying concepts can still be quite hard.

What subject are you studying?

 

[aaaa202]

Physics..? :P Pure physics with a lot of focus on the math.

 

[Studiot]

Physics

Well before you can answer the question

What happens when the plank begins to rotate?

You have to show that it will rotate.

So a logical question sequence is

Will it rotate?
How far will it rotate?

These are really 'force' questions.

Then we can ask

How fast will it rotate?

This is an energy question

Then we can ask the more difficult one

What happens as it rotates, to speed, energy etc?

 

[aaaa202]

Yes that was pretty much the conclusion I came to.

You shouldn't make direct parallels between force and energy. Problem is though that I can only understand torque (which I see as a rotational analogue to a force) through energy.

But that is perhaps becaues I'm too eager to want to explain torque through things I already know, rather than accepting, that it is a new concept.

 

[Studiot]

Well let us not forget energy, I did say that we would discuss this soon.

In case (1) energy consideration is fairly simple.

Work is done since a force has moved its point of application.

Can you complete this with some figures, otherwise I am doing all the work (pun intended) here.

 

[aaaa202]

umm sure, though I don't know what you are exactly looking for.
In case #1 where F=0.
The torque on the rod will make it rotate downwards - here it is obvious to me why torque considerations work, since the center of mass will also have to translate downwards.

Since the cross product of W and L, where L is the distance vector from the pivot to the center of mass of the rod, will get smaller and smaller, the angular acceleration will do the same.
For small angles this would make a physical pendulum since sin(θ) ≈ θ for a little angular displacement.

Is this what you were looking for? I can do all this, I just need to understand torque as a concept.

In case #2 the same thing should happen but with of course different numbers, assuming that F is always applied perpendicular to the rod.

In case #3 the rod is not in rotational equilibrium since there is a torque around the center of mass. Thus the rod will rotate upwards pushing up against the hinge. This will in turn make the rod rotate downwards as we would expect.

I just want to understand torque.

 

[Studiot]

Actually you didn't mention energy or work once.

The force W moves down a distance equal to L₂.

Thus work done = force times distance = WL₂

This equals the loss of potential energy of the plank.

This can be equated to the kinetic energy of the plank.

If you like you can develop a more complicated equation connecting the conversion of potential energy to KE by the motion of the plank.
However we all know that this is just the motion of a pendulum of weight W suspended from a light rod or string of length L₂.

In the absence of friction or other restraining force this interchange will go on forever as the plank swings upward past vertical to the horizontal the other way and so on.

 

[aaaa202]

hmm yes, I could've done that, but all of this is really trivial and not what I want to understand.

So let's for the last time try to consider when F=W.
The Center of Mass is in equilibrium until the hinge pushes down on the rod. In order for it to do that the torque somehow has to make the rod push against the upper end.
But in my universe a torque can't do that, because a torque is only something that works, when an object is in motion.

But my understanding of torque is wrong, and I think I'll read up on some other books, that present the subject more clear. I've asked my instructors and teachers, and they were not able to answer my question, unless you took some empirical knowledge for granted.

 

[Studiot]

You have been told several times by several responders that the case of F=W is not an equilibrium case as you have presented it.

If you worked through my cases, rather than dismissimg my comments as trivial, until you reached this one you would prove that.

You need to try to appreciate the universe as it is not as you would like it to be to fit your own theories.
That approach will become increasingly counterproductive as your studies progress.

 

[aaaa202]

I perfectly understand it's not an equilibrium. Did I say otherwise?

The sum of torques is non-zero making the pivot exert a downwards force. I'll try to read through them again, but really I got nothing than that from the posts.

But equilibrium is just a word. If I push on the end of a wrench it will translate and rotate. I just don't understand what initiates rotation.

I do NOT make my own theories. I always accept how the equations look, but that shouldn't prevent me from trying to understand them through familiar concepts.

If the notion of an equilibrium lies in the way I present the case, can you try to present it step for step the way you would.

The one thing I learned was the remark about signal propagating through objects at the speed of sound.

 

[Studiot]

Some of this is very basic stuff and has also been mentioned indirectly by others.

If you have a pair of masses there is a gravitational force between them. No energy is required to initiate or maintain this force.

You can say the same about the reaction forces between your table and the glass of beer on it.
However these forces only appear as needed, unlike gravity, which no one except scifi authors has ever got away from.

Energy (only) becomes involved when something changes and work is done.

Rotational effects are similar.
Torque or moment may always be present in a system or appear as a reaction when necessary.

No energy is required for this.
Energy does become involved when something changes rotationally.