Daz50
- 2
- 0
Homework Statement
Dear Physics Forums, I was hoping you may be able to help with a problem I am having in my final postgraduate project.
A short background of the project to put the problem into context - I am designing and manufacturing a form of powered orthosis to help a person move from a sitting position to a standing position.
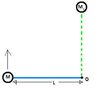
I am currently trying to calculate the forces involved in the sit-to-stand tranition. For simplicity at this stage, my image shows a very basic model I created of a mass on the end of a moment arm.
The attached file shows an image of this simple model.
The mass, M (90kg) is designed to represent a person's bodyweight, the length L (65.8cm) is the buttock-knee length of a person and the pivot point O, represents the knee joint. Anything below the knee is disregarded at this stage. The mass M is required to travel 90degrees in 1.5 seconds, finishing at M1 (the green dashed line) assuming a constant angular velocity. It is also on a vertical plain as this is supposed to model someone standing up.
Homework Equations
Torque = I Alpha (The equation I think I should be using but I am not sure how)
Torque = mass x Alpha x L2 (The equation I actually used but I think is wrong)
The Attempt at a Solution
My working so far is as follows:
1) convert 90degrees into radians 90 / (pi/2) = 1.575 radians
2) Work out how many radians per second 1.575 radians / 1.5 seconds = 1.05r/s
3) Factor in the mass M, and the length, L into the equation.
90kg x 1.05rad/s x 0.658m2 = 40.9Newton Metres.
I have a calculated value of 40.9Newton metres to move the 90kg mass through 90degrees, however I am not sure how to factor the effects of gravity into this equation as this would certainly have an impact on the torque required to move M to M1.
Apologies if this post is a bit all over the place - I do not have a physics background because I came from a different undergrad degree discipline so am trying my best!
Any assistance would be appreciated!
Kind regards,
Daz
Attachments
Last edited: