PeachBanana
- 189
- 0
Homework Statement
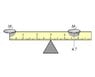
A centimeter ruler, balanced at its center point, has two coins placed on it, as shown in the figure. One coin, of mass 10 g , is placed at the zero mark; the other, of unknown mass , is placed at the 4.7 cm mark. The center of the ruler is at the 3.0 cm mark. The ruler is in equilibrium; it is perfectly balanced.
Find the unknown mass.
Homework Equations
τ = F * r
The Attempt at a Solution
I set the zero mark to be in a center of the ruler. Then I tried to compute the counterclockwise Torque.
τ = (0.01 kg)(0.03 m)(9.8 m/s^2)
I'm really unsure about using the acceleration due to gravity. Should I have been using τ = Iα instead? I figure if I know how to properly find the counterclockwise torque, the clockwise torque will follow the same method.