A Total force generated in a pneumatic cylinder-piston with kn

[foadsf]

I have also asked this question in SO and CFD online

Assuming that we have a pneumatic cylinder-piston with arbitrary but known surface area A, a known clarence c, and a known length L. What is the best model to describe the total steady state force applied on the piston considering the leakage? (the force required to keep the piston in place)

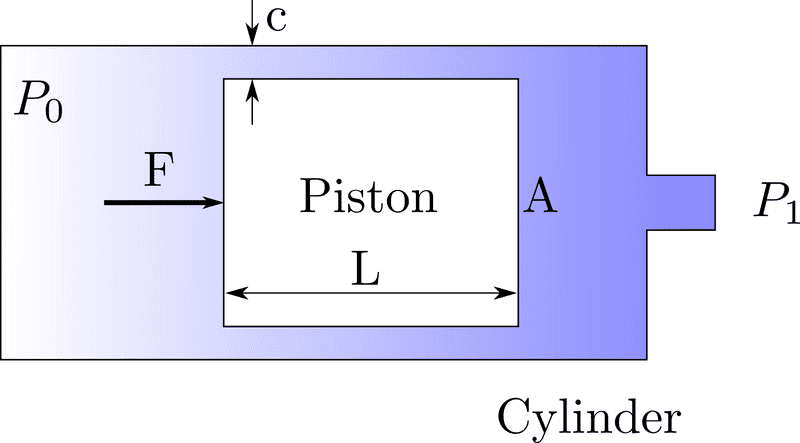What I'm looking for is an equation in the form of $F=f\left(P_1,A, L, c\right)$. In extreme cases:

- if $c\rightarrow 0$ then $F=P_1A$ is just hydrostatic pressure
- if c is big then $F\approx \frac{1}{2}\rho\nu^2C_DA$ is just air drag

I can calculate leakage from empirical or theoretical models but I don't know how to proceed from there.

 

[Nidum]

Given that the piston is not moving and that there is at least some leakage of air possible around the piston then :

When the system is in steady state condition P₀ = P₁ and F = 0

When the system is in transient condition P₀ is initially < P₁ but increases with time as air flows around the piston . To a good approximation at any time t during this transient period F = (P₁ - P₀ at time t) x A .

The value of P₀ at time t can be determined using standard air flow calculation methods .

You could calculate the viscous air drag force on the piston at time t as well but it is likely to be insignificant in many practical cases .