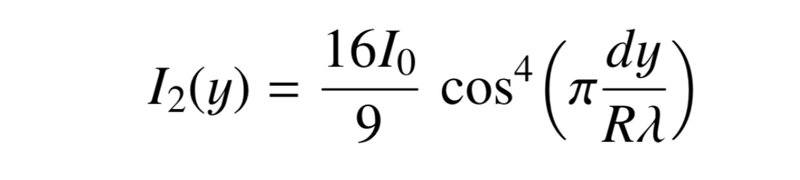SUMMARY
The discussion focuses on calculating the time-average intensity of light from three slits using the equation for the electric field amplitude, represented as ##E(y,t) = Asin(1+2cos(\frac {2\pi dy}{R\lambda}))sin(ωt + α)##. Participants clarify that intensity is proportional to the square of the amplitude, leading to the expression for time-averaged intensity being ##_{time} = ½A^2sin^2(1+2cos( \frac {2\pi dy}{R\lambda}))##. The maximum value of the amplitude squared is determined to be 9, which necessitates dividing the total intensity ##I_0## by 9 to account for the contributions from all slits. The discussion emphasizes the importance of understanding the averaging process and the role of the sine function in calculating the time-average intensity.
PREREQUISITES
- Understanding of wave mechanics and interference patterns
- Familiarity with electric field amplitude equations
- Knowledge of trigonometric functions and their properties
- Basic principles of intensity and time averaging in wave physics
NEXT STEPS
- Study the derivation of the electric field amplitude for multiple slits
- Learn about the principles of wave interference and diffraction
- Explore the mathematical properties of sine and cosine functions in wave equations
- Investigate the relationship between amplitude and intensity in wave physics
USEFUL FOR
Students and professionals in physics, particularly those focusing on optics and wave mechanics, as well as educators seeking to deepen their understanding of interference patterns in multi-slit experiments.