Traditional double Atwood's machine

[rahuldandekar]

Ok, I can understand this problem, I have read it's solution, can see how it is arrived at... but I can't understand WHY it is true.

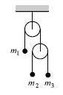
It's a traditional double Atwood's machine... have to find the accelerations of the three particles.

I can understand how they got the equations, for the second pulley, T1 = 2*T2. The force equations for the masses are straightforward too. The "conservation of string" equation is... a1 = -(a2 + a3)/2 which is.... ok, I guess.

But, I have trouble understanding the solution. For, the acceleration of m1 is
a1 = g*(4*m2*m3 - m1*(m2+m3))/(4*m2*m3 + m1*(m2+m3)).

Now, What if I imagine the pulley 2 system as a black box, of mass m2+m3?

I'll get the equation for a1 as g*(m1 - (m2+m3))/(m1+m2+m3) .
So, why can't we imagine the second system as a black box?

There's some obvious reason here, I'm sure, but I just can't get it. :(

 

[Doc Al]

You cannot replace the 2nd pulley system with a single mass equal to m2 + m3. For one thing, m2 and m3 have different accelerations, while your replacement mass would have only one.

 

[rahuldandekar]

Ok... thanks... I'm also thinking that maybe it's because T1 is determeined by T2...