Mitchy190
- 42
- 0
I'm trying to work out the Transfer function for the 2nd order RC circuit in the attachment below: I can't seem to get the right answer :(
circuit:
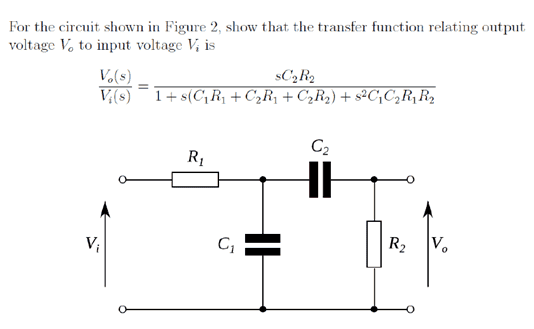
My answer:
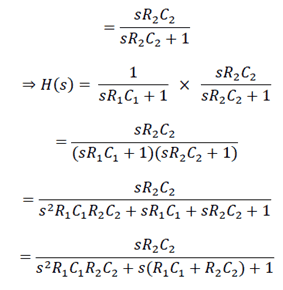
Please see attachment for my attempt and the relevant information:
View attachment f.pdf
circuit:
My answer:
Please see attachment for my attempt and the relevant information:
View attachment f.pdf
Last edited: