Transfer function of this simple circuit

[Screwdriver]

Homework Statement

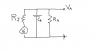
The picture of the circuit is attached; I want to find |V_{A}/V_{J}|. This seems really easy but I haven't done circuit analysis in forever.

Homework Equations

Complex impedances, Z_{C} = 1/i\omega C, Z_{R} = R.

The Attempt at a Solution

First R_{A} and C_{A} are in parallel, so the equivalent impedance is Z_{A} = Z_{C_{A}} Z_{R_{A}} /(Z_{C_{A}} + Z_{R_{A}}). Then the circuit is a voltage divider, so the voltage across Z_{A} is V_{A} = V_{J} Z_{A}/(Z_{A} + Z_{R_{J}}). Therefore,

$$
\frac{V_{A}}{V_{J}} = \frac{Z_{A}}{Z_{A} + Z_{R_{J}}} = \frac{i R_{A}}{i(R_{A} + R_{J}) - C_{A} R_{A} R_{J} \omega} \implies \left| \frac{V_{A}}{V_{J}} \right| = \frac{R_{A}}{\sqrt{(R_{A} + R_{J})^2 + (C_{A} R_{A} R_{J} \omega)^2}}
$$

 

[gneill]

Looks good.

 

[Screwdriver]

Okey dokey, thank you!