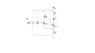
Full analysis of this type of a circuit is not so easy.
But let as first assume that Q1 is Cut-off and Q2 is in saturation region.
So to open Q1 the voltage at Q1 base must be Vbe larger then emitter voltage.
So the first think we need to do is to find a voltage across RE resistor (Ve) when Q1 is OFF and Q2 in saturation region.
We know that emitter current is always (even in saturation) equal to
Ie = IB + IC
So we have
Ie = Ve/RE
Ib = (Vcc - Vbe - Ve))/R2
Ic = (Vcc - Vd - Vce(sat) - Ve)/Rc
Where
Vcc = 5V; Vd = 2V --->LED forward voltage drop
Vbe = 0.7V
Vce(sat) - Vce saturation voltage ---> 0.1V.
Ve/RE = (Vcc - Vbe - Ve))/R2 + (Vcc - Vd - Vce(sat) - Ve)/Rc
And now if we solve this for VE we have this
\Large Ve = (\frac{Vcc - Vbe}{R2} + \frac{Vcc - Vd - Vce_{sat}}{RC}) * R2||RC||RE
\Large Ve = 1.42V
So Q1 will start to conduct if voltage at Q1 base is larger than
Ve + Vbe ≈ 2.12V.
Q1 will also starts to steal some R2 current from Q2 base. As the input voltage rising Q1 switches from Cutt-off to saturation and Q2 switch from saturation to cutt-off.
Q2 will start to comes out form saturation for the base current smaller than.
IB2 < Ic2_sat/Hfe
Ic2_sat = (Vcc - Vd - Vce_sat - Ve)/Rc = (5V - 2V - 0.1V - 1.42V)/250Ω ≈ 1.5V/250Ω = 6mA
IB2 = 6mA/200 = 30μA
So the IC1 is now equal to
Ic1 = IR2 - IB2 ≈ IR2
IR2 = (5V - 0.7V - 1.42V)/850Ω ≈ 3.3mA
Ans this Ic current caused by IB1 current equal to:
IB1 = Ic/Hfe = 3.3mA/200 = 16.5μA. And this base current will flow through RB resistor and
causes a voltage drop.
VRB = IB*RB ≈ 0.38V
So now we have all information needed to find upper threshold voltage.
Vt2 = Ve + Vbe1 + VRB ≈ 2.5V
Now let as try to find a lower threshold voltage.
We have Q1 in saturation and Q2 in cut-off. So to open Q2 Vce1 voltage mus be larger than Vbe2.
Ic = Ie = (Vcc - Vbe)/(R2+RE) = 4.4mA and Ve = 0.660V.
If the voltage at Q1 base is smaller than Ve + Vbe1 = 0.660V + 0.7V = 1.36V Q1 starts comes out form saturation region. This will happen for the base current equal to
IB1 = Ic/Hfe = 4.4mA/200 = 22μA. This current will give as a voltage drop across RB equal to:
VRB = 0.5V.
And the lower threshold voltage is equal to:
Vt1 = Ve + Vbe + VRB = 0.66V + 0.7V + 0.5V = 1.86V
Designing this circuit also is ton easy task. And this is why we almost always use a op amp as a Schmitt trigger or we add more resistors.
http://www.johnhearfield.com/Eng/Schmitt.htm