norbellys
- 5
- 1
1. Homework Statement
I am trying to solve a triple integral using cylindrical coordinates. This is what I have to far . But I think I have choosen the limits wrong.
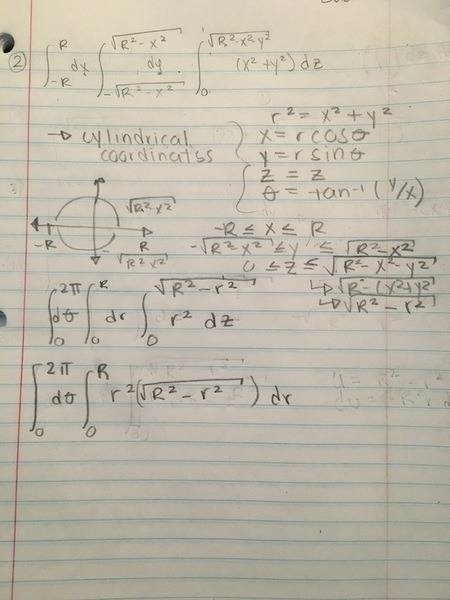 [/B]
[/B]
I am trying to solve a triple integral using cylindrical coordinates. This is what I have to far . But I think I have choosen the limits wrong.