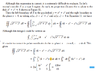Triple integration - find volume

[yecko]

Homework Statement

Homework Equations

in the pic

The Attempt at a Solution

why is there an extra "r" in the highlighted line?

my attempt:
$\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ d\theta$
= $\int_0^{2\pi}\int_0^2\left(4-r^2\right)\ r\ dr\ d\theta$

thanks

 

[NFuller]

why is there an extra "r" in the highlighted line?

Because it is part of the correct form of the differential area in polar coordinates.
$$dA=r\;dr\;d\theta$$

 

[yecko]

$\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ d\theta$

I have considered r dr dθ already in my calculation... but the answer is r *r *dr*dθ

 

[Mark44]

I have considered r dr dθ already in my calculation... but the answer is r *r *dr*dθ

It comes from the substitutions for polar coordinates in the x-z plane, for the expression $\sqrt{x^2 + z^2}$. This is explained in the example where they use $x = r\cos(\theta)$ and $z = r\sin(\theta)$.

 

[yecko]

√x^2+z

but why is there exists this expression in the first line of the second pic?
isn't that always 1 in the middle and integrate by looking at the boundaries for the triple integration?

my attempt : $\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ dθ$
mechanism: I would like to get the height first, then get the area of the cylinder

(my concepts are a little bit messy... sorry for that... and thank you very much for your patience)

 

[Mark44]

but why is there exists this expression in the first line of the second pic?
isn't that always 1 in the middle and integrate by looking at the boundaries for the triple integration?
my attempt : $\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ dθ$

(my concepts are a little bit messy... sorry for that... and thank you very much for your patience)

If the goal is to find the volume using a triple integral, then the integrand will be 1, something like this $\iiint_E 1~dV$.
However, in this problem you are asked to evaluate an integral that doesn't represent a volume.

 

[yecko]

the solution: $\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$
so why the solution put r in the middle?

 

[Mark44]

the solution: $\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$
so why the solution put r in the middle?

I don't know what you're talking about. The solution in the example you posted doesn't have y in it. They converted the integral to polar form - no x, y, or z.

 

[yecko]

I don't know what you're talking about. The solution in the example you posted doesn't have y in it. They converted the integral to polar form - no x, y, or z.

its the same...
$\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$ =$\int_0^{2\pi}\int_0^2\left(4-r^2\right)r\ \ r\ dr\ dθ$

so why the solution put r in the middle?

 

[Mark44]

its the same...
$\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$ =$\int_0^{2\pi}\int_0^2\left(4-r^2\right)r\ \ r\ dr\ dθ$

so why the solution put r in the middle?

I don't know. It seems that you put it in the middle, since the textbook image you posted doesn't have this integral in it - $\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$.

You could rewrite that integral like so: $\int_0^{2\pi}\int_0^2\int_{r^2}^4\ dy\ r^2\ dr\ dθ$, and it wouldn't make any difference - you get the same integral as shown on the right in what I quoted from you.

 

[yecko]

But why not$\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ dθ$ which is 1 in the middle?
why is solution is $\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$ = $\int_0^{2\pi}\int_0^2\left(4-r^2\right)r\ \ r\ dr\ dθ$ ?

However, in this problem you are asked to evaluate an integral that doesn't represent a volume

it is asking for volume in the question...

 

[Mark44]

But why not$\int_0^{2\pi}\int_0^2\int_{r^2}^41\ dy\ r\ dr\ dθ$ which is 1 in the middle?

You keep asking this question, which was answered in posts #2 and #4. What parts of those posts do you not understand?

why is solution is $\int_0^{2\pi}\int_0^2\int_{r^2}^4r\ dy\ r\ dr\ dθ$ = $\int_0^{2\pi}\int_0^2\left(4-r^2\right)r\ \ r\ dr\ dθ$ ?it is asking for volume in the question...

NO, IT IS NOT!
As it says in the image you posted,

Evaluate $\iiint_E \sqrt{x^2 + z^2}~dV$, where E is the region bounded by the paraboloid $y = x^2 + z^2$ and the plane $y = 4$.

This is NOT a volume integral!

Please take more care in your reading.

 

[yecko]

If the goal is to find the volume using a triple integral, then the integrand will be 1, something like this $\iiint_E 1~dV$.
However, in this problem you are asked to evaluate an integral that doesn't represent a volume.

it is not a volume, so it is just a physically-meaning mathematics expression?
i see. thanks for telling me.