axemaster
- 58
- 7
OK, so I'm trying to build a hyper-fast rotating disk, probably of aluminum. The tensile strength is about 200MPa (note that this is a pressure, which makes sense), and I'm trying to calculate the tensile pressure throughout the disk. The point being to find out how fast I can spin the thing before it tears apart due to the centifugal force. To phrase it more succinctly:
A disk of radius R and mass density ρ rotates about its axis with angular frequency ω. Find the tensile pressure at radius r_o.
So I started out by finding the infinitesimal outward force exerted by successive rings of material:
v=ωr
a=v^{2}/r
→ a=ω^{2}r
And the mass of each ring is:
→ dm=2\pi rh*ρ*dr ---------- note that "h" is the thickness, included to make it a volume
The infinitesimal force on each ring segment is then:
dF=dm*a
→ dF=2\pi r^2 ω^2 h ρ dr
Now I integrated the force from the radius of interest r_o, to the outer radius "R". This should give us the total force the material must withstand at radius r_o.
F=\int^{R}_{r_o} 2\pi r^2 ω^2 h ρ dr
F=2\pi ω^2 h ρ (\frac{R^3}{3}-\frac{r^{3}_{o}}{3})
When plotted in Mathematica (setting all variables to 1 and varying r_o) this looks like:

This appears to be correct. As one might expect, the force starts at zero on the outer edge and increases to a more or less constant value at the center.
The trouble starts when I tried to convert this into a pressure by dividing by the area at r_o.
→ A=2\pi r_o h
→ Pressure=F/A=\frac{ω^2 ρ (\frac{R^3}{3}-\frac{r^{3}_o}{3})}{r_o}
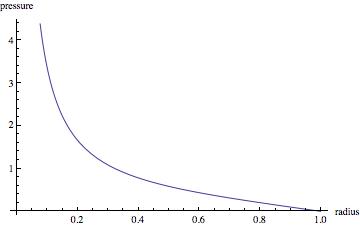
As you can see, the pressure goes to infinity at the center. This is clearly wrong, but I'm not sure how to fix it. Please help!
A disk of radius R and mass density ρ rotates about its axis with angular frequency ω. Find the tensile pressure at radius r_o.
So I started out by finding the infinitesimal outward force exerted by successive rings of material:
v=ωr
a=v^{2}/r
→ a=ω^{2}r
And the mass of each ring is:
→ dm=2\pi rh*ρ*dr ---------- note that "h" is the thickness, included to make it a volume
The infinitesimal force on each ring segment is then:
dF=dm*a
→ dF=2\pi r^2 ω^2 h ρ dr
Now I integrated the force from the radius of interest r_o, to the outer radius "R". This should give us the total force the material must withstand at radius r_o.
F=\int^{R}_{r_o} 2\pi r^2 ω^2 h ρ dr
F=2\pi ω^2 h ρ (\frac{R^3}{3}-\frac{r^{3}_{o}}{3})
When plotted in Mathematica (setting all variables to 1 and varying r_o) this looks like:
This appears to be correct. As one might expect, the force starts at zero on the outer edge and increases to a more or less constant value at the center.
The trouble starts when I tried to convert this into a pressure by dividing by the area at r_o.
→ A=2\pi r_o h
→ Pressure=F/A=\frac{ω^2 ρ (\frac{R^3}{3}-\frac{r^{3}_o}{3})}{r_o}
As you can see, the pressure goes to infinity at the center. This is clearly wrong, but I'm not sure how to fix it. Please help!